Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 325
Задание 325
\[\boxed{\mathbf{325.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
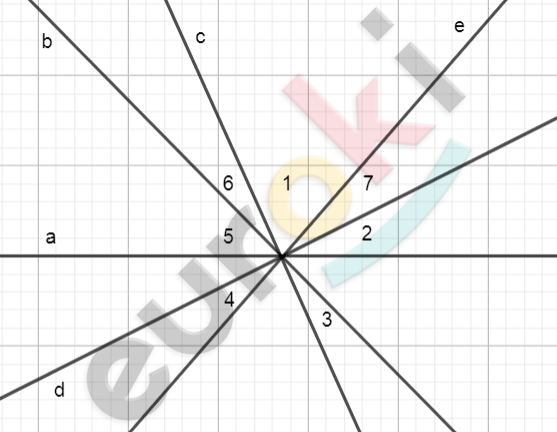
\[Дано:\]
\[a \cap b \cap c \cap d \cap e = O.\]
\[Найти:\ \]
\[\angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 - ?\]
\[Решение.\]
\[1)\ \angle 3 = \angle 6\ \]
\[(как\ вертикальные\ углы).\]
\[2)\ \angle 4 + \angle 7\ \]
\[(как\ вертикальные\ углы).\]
\[3)\ \angle 5 + \angle 6 + \angle 1 + \angle 7 + \angle 2 =\]
\[= 180{^\circ}\ (как\ смежные\ углы).\]
\[4)\ Получаем:\]
\[\ \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 =\]
\[= \angle 1 + \angle 2 + \angle 6 + \angle 7 + \angle 5 =\]
\[= 180{^\circ}.\]
\[Ответ:180{^\circ}.\]
\[\boxed{\mathbf{325.еуроки - ответы\ на\ пятёрку}}\]
\[\mathbf{Дано:}\]
\[b - медиана;\]
\[a - высота;\]
\[c = AB.\]
\[Построить:\ \]
\[\mathrm{\Delta}ABC.\]
\[Построение.\]
\[1)\ Построим\ две\ параллельные\ прямые\ на\ расстоянии\ \text{a.}\]
\[2)\ На\ одной\ из\ них\ отложим\ отрезок\ AB = c.\]
\[3)\ Построим\ окружность\ (A;2b),\ на\ пересечении\ этой\ окружности\]
\[и\ второй\ прямой\ отметим\ точку\ \text{D.}\]
\[4)\ Отметим\ точку\ M - середину\ \text{AB.}\]
\[5)\ Построим\ луч\ BM,\ на\ пересечении\ данного\ луча\ и\ второй\ прямой\]
\[отметим\ точку\ \text{C.}\]
