Решебник по геометрии 7 класс Атанасян ФГОС Задание 323

 

\[\boxed{\mathbf{323.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\]

\[AB = m \bullet E_{1}F_{1};\ \]

\[AB = n \bullet E_{2}F_{2};\]

\[E_{1}F_{1} = a \bullet E_{2}F_{2}.\]

\[Найти:\]

\[a - ?\]

\[Решение.\]

\[1)\ AB = m \bullet E_{1}F_{1}\ и\ \]

\[AB = n \bullet E_{2}F_{2}:\]

\[\ m \bullet E_{1}F_{1} = n \bullet E_{2}F_{2}.\]

\[2)\ E_{1}F_{1} = \frac{n}{m} \bullet E_{2}F_{2}:\]

\[a = \frac{n}{m}.\]

\[Ответ:длина\ отрезка\ E_{1}F_{1}\ \]

\[выражается\ числом\frac{n}{m}\text{.\ }\]

\[\boxed{\mathbf{323.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Построить\ прямоугольный\ треугольни}к\ ABC.\]

\[\mathbf{а)\ по\ гипотенузе\ и\ острому\ углу:}\]

\[1)\ На\ одной\ из\ сторон\ угла\ откладываем\ отрезок\ \text{AB\ }равный\ \text{a.}\]

\[2)\ Из\ точки\ B\ строим\ перпендикуляр\ ко\ второй\ стороне\ угла.\]

\[3)\ На\ пересечении\ перпенидкуляра\ и\ стороны\ отмечаем\ точку\ \text{C.}\]

\[\textbf{б)}\ по\ катету\ и\ противолежащему\ углу:\]

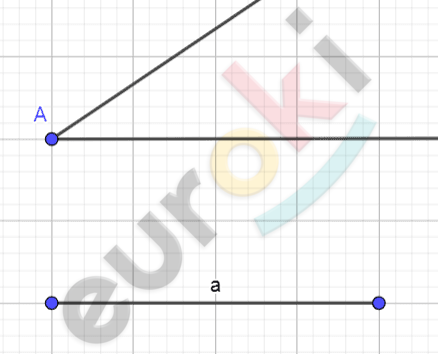
\[1)\ На\ одной\ из\ сторон\ угла\ отмечаем\ случайно\ точку\ C_{1},\]

\[восстанавливаем\ из\ этой\ точки\ перпендикуляр\ и\ отложим\ \]

\[отрезок\ C_{1}B_{1} = a.\]

\[2)\ Из\ точки\ B_{1}\ строим\ перпендикуляр\ к\ C_{1}B_{1}\ и\ отметим\ точку\]

\[\text{B\ }на\ пересечении\ перпендикуляра\ и\ второй\ стороны\ угла.\]

\[3)\ Из\ точки\ B\ строим\ перпендикуляр\ ко\ второй\ стороне\ угла.\]

\[4)\ На\ пересечении\ перпендикуляра\ и\ стороны\ отмечаем\ точку\ \text{C.}\]

\[\textbf{в)}\ по\ гипотенузе\ и\ катету:\]

\[1)\ Строим\ прямую\ и\ отмечаем\ на\ ней\ отрезок\ BC = a.\]

\[2)\ В\ точке\ \text{C\ }восстанавливаем\ перпендикуляр\ к\ данной\ прямой.\]

\[3)\ Строим\ окружность(B;c),\ на\ пересечении\ окружности\ и\]

\[перпендикуляра\ отмечаем\ точку\ \text{A.}\]