Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 201
Задание 201
\[\boxed{\mathbf{201.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ \mathbf{\ задачи:}\]
\[Дано:\]
\[a \parallel b;\]
\[c - секущая;\]
\[\angle 2 + \angle 5 = 210{^\circ}.\]
\[Найти:\]
\[\angle 1;\ \angle 2;\ \angle 3;\ \angle 4;\]
\[\angle 5;\angle 6;\angle 7;\angle 8 - ?\]
\[Решение.\]
\[1)\ a \parallel b \rightarrow \angle 2 =\]
\[= \angle 5\ (как\ накрест\ лежащие);\]
\[\angle 2 = \angle 5 = 210{^\circ}\ :2 = 105{^\circ};\]
\[2)\ \angle 1 = \angle 2 =\]
\[= 105{^\circ}\ (как\ вертикальные);\]
\[\angle 5 = \angle 6 =\]
\[= 105{^\circ}\ (как\ вертикальные);\]
\[3)\ \angle 7 = 180{^\circ} - \angle 5 =\]
\[= 180{^\circ} - 105{^\circ} =\]
\[= 75{^\circ}\ (как\ смежные);\]
\[\angle 8 = 180{^\circ} - \angle 6 =\]
\[= 180{^\circ} - 105{^\circ} =\]
\[= 75{^\circ}\ (как\ смежные);\]
\[\angle 3 = 180{^\circ} - \angle 1 =\]
\[= 180{^\circ} - 105{^\circ} =\]
\[= 75{^\circ}\ (как\ смежные);\]
\[\angle 4 = 180{^\circ} - \angle 2 =\]
\[= 180{^\circ} - 105{^\circ} =\]
\[= 75{^\circ}\ (как\ смежные).\]
\[Ответ:\ \angle 1 = \angle 2 = \angle 5 = \angle 6 =\]
\[= 105{^\circ};\ \]
\[\ \angle 7 = \angle 8 = \angle 3 = \angle 4 = 75{^\circ}.\]
\[\boxed{\mathbf{201.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\ \]
\[\mathbf{Дано:}\]
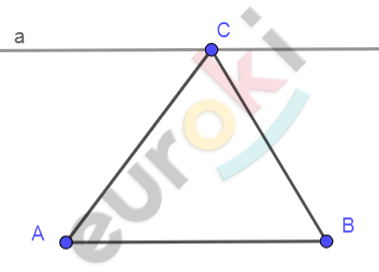
\[\mathrm{\Delta}\text{ABC}.\]
\[\mathbf{Найти:}\]
\[сколько\ прямых,\]
\[\parallel \text{AB},\ можно\ \]
\[провести\ через\]
\[точку\ C.\]
\[\mathbf{Решение.}\]
\[Через\ точку\ \text{C\ }можно\ провести\ \]
\[только\ одну\ прямую\ a \parallel \text{AB\ }\]
\[(аксиома\ о\ параллельности\]
\[прямых).\]
