Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 186
Задание 186
\[\boxed{\mathbf{186.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[106.\]
\[\mathbf{Дано:}\]
\[a;b - прямые;\]
\[c - секущая;\]
\[\textbf{а)}\ \angle 1 = 37{^\circ};\]
\[\ \angle 7 = 143{^\circ};\]
\[\textbf{б)}\ \angle 1 = \angle 6;\]
\[\textbf{в)}\ \angle 1 = 45{^\circ};\ \]
\[\angle 7 = 3 \cdot \angle 3.\]
\[\mathbf{Доказать:}\]
\[a \parallel b.\]
\[\mathbf{Доказательство.}\]
\[\textbf{а)}\ Односторонние\ углы\]
\[равны\ 180{^\circ}:\]
\[\angle 1 + \angle 7 = 180{^\circ}.\]
\[Проверим:\ \ \]
\[37 + 143 = 180{^\circ}\ (верно).\]
\[Значит,\ по\ признаку\ \]
\[параллельности\ прямых,\ \]
\[получаем:\]
\[a \parallel b.\]
\[\textbf{б)}\ \angle 1 = \angle 6 - как\ накрест\ \]
\[лежащие:\]
\[по\ признаку\ параллельности\ \]
\[прямых \rightarrow \ a \parallel b.\ \]
\[\textbf{в)}\ По\ условию:\]
\[\angle 1 + \angle 7 =\]
\[= 180{^\circ}\ (как\ односторонние\ углы);\]
\[\angle 1 = \angle 3\ (как\ ветрикальные).\]
\[Получаем:\]
\[\angle 1 + 3\angle 1 = 180{^\circ}.\]
\[Следовательно:\]
\[\ 4\angle 1 = 180{^\circ} \rightarrow \angle 1 = 45{^\circ};\]
\[\angle 7 = 3 \cdot 45 = 135{^\circ}.\]
\[Проверяем:\ \]
\[\angle 1 + \angle 7 = 45 + 135 =\]
\[= 180{^\circ} - верно.\]
\[По\ признаку\ параллельности\ \]
\[прямых:\]
\[a \parallel b.\ \]
\[Что\ и\ требовалось\ доказать.\]
\(\boxed{\mathbf{186.еуроки - ответы\ на\ пятёрку}}\)
\[Дано:\]
\[A;B;\]
\[\text{PQ.}\]
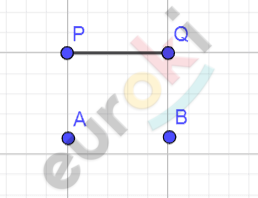
\[Построить:\]
\[окружность\ (O;PQ);\]
\[A \in окружности;\ \ \]
\[B \in окружности.\]
\[Построение.\]
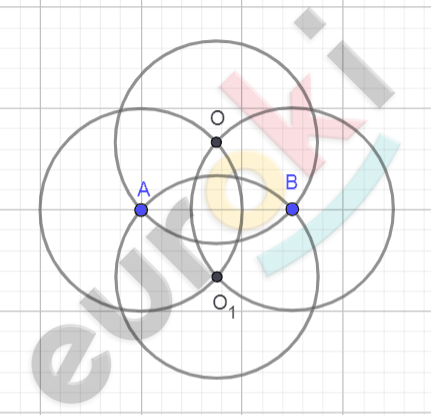
\[Построим\ две\ окружности:\]
\[(A;PQ)\ и\ (B;PQ).\]
\[Получим\ их\ пересечение\ \]
\[в\ точке\ O\ и\ точке\ O_{1};\]
\[или\ только\ в\ точке\ O;\]
\[или\ не\ пересекаются\ совсем.\]
\[І\ случай:\ \]
\[ІІ\ случай:\]
\[ІІІ\ случай:\]
