Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 169
Задание 169
\[\boxed{\mathbf{169.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:95.\]
\[Дано:\]
\[OC = OD;\]
\[OB = OE.\]
\[Доказать:\]
\[AB = EF.\]
\[Доказательство.\]
\[1)\ \mathrm{\Delta}BOC = \mathrm{\Delta}DOE - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[BO = OE\ (по\ условию);\]
\[CO = OD\ (по\ условию);\]
\[\angle BOC = \angle DOE\ \]
\[(как\ вертикальные).\]
\[Значит:\]
\[\angle CBO = \angle OED.\]
\[2)\ \angle ABO = \angle OEF:\]
\[\angle ABO = 180 - \angle CBO\ \]
\[(смежные\ углы);\]
\[\angle OEF = 180 - \angle OED\ \]
\[(смежные\ углы);\]
\[\angle CBO = \angle OED\ (см.\ пункт\ 1).\]
\[3)\ \mathrm{\Delta}ABO = \mathrm{\Delta}OEF - \ по\ стороне\ \]
\[и\ двум\ прилежащим\ к\ ней\ \]
\[углам:\ \]
\[BO = OE\ (по\ условию);\]
\[\angle ABO = \angle OEF\ (см.\ пункт\ 2);\]
\[\angle AOB = \angle EOF\ \]
\[(как\ вертикальные).\]
\[Следовательно:\ \]
\[AB = EF.\]
\[Что\ и\ требовалось\ доказать.\]
\[\boxed{\mathbf{169.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равносторонний;\]
\[AB = BC = AC;\]
\[AD = FC = EB;\]
\[E \in AB;F \in BC;\ \]
\[D \in AC.\]
\[\mathbf{Доказать:}\]
\[\mathrm{\Delta}DEF - равносторонний.\]
\[\mathbf{Доказательство.}\]
\[1)\ По\ условию:\]
\[AB = BC = AC;\ \ \]
\[AD = EB = FC.\]
\[Отсюда:\]
\[AE = BF = DC.\]
\[2)\ \mathrm{\Delta}AED = \mathrm{\Delta}EBF = \mathrm{\Delta}DFC -\]
\[по\ двум\ сторонам\ и\ углу\ \]
\[между\ ними:\]
\[AD = EB = FC\ (по\ условию);\]
\[AE = BF = DC\ (см.\ пункт\ 1);\]
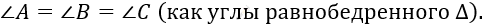
\[3)\ Значит,\ в\ треугольнике\ \text{DEF\ }\]
\[все\ стороны\ \]
\[3)\ Получаем:\ \]
\[ED = DF = EF.\]
\[Следовательно:\ \]
\[\mathrm{\Delta}DEF - \ равнобедренный.\]
\[Что\ и\ требовалось\ доказать.\]
