Решебник по геометрии 7 класс Атанасян ФГОС Задание 168

 

\[\boxed{\mathbf{168.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[\angle A = 38{^\circ};\ \]

\[\angle B = 110{^\circ};\]

\[\angle C = 32{^\circ};D \in AC;\]

\[E \in AC;\ \ BD = DA;\]

\[BE = EC.\]

\[\mathbf{Найти:}\]

\[\angle DBE = ?\]

\[\mathbf{Решение.}\]

\[1)\ AD = DB\ (по\ условию),\ \]

\[поэтому:\]

\[\ \mathrm{\Delta}ADB - равнобедренный.\ \]

\[Значит,\ углы\ при\ основании\ \]

\[равны:\ \ \]

\[\angle A = \angle DBA = 38{^\circ}.\]

\[2)\ EB = EC\ (по\ условию);\ \ \]

\[тогда:\ \ \]

\[\mathrm{\Delta}BEC - \ равнобедренный.\]

\[Значит,\ углы\ при\ основании\ \]

\[равны:\]

\[\angle C = \angle EBC = 32{^\circ}.\]

\[3)\ \angle B = \angle ABD + \angle DBE + \angle EBC\]

\[\angle DBE = 110 - 32 - 38 =\]

\[= 110 - 70 = 40{^\circ}.\]

\[Ответ:\ \angle DBE = 40{^\circ}.\]

\[\boxed{\mathbf{168.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равнобедренный;\]

\[AE = EB;\]

\[BF = FC;\]

\[AD = DC.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}DEF - равнобедренный.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}AED = \mathrm{\Delta}DFC - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[AD = DC\ (по\ условию);\]

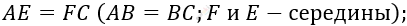
\[\angle A = \angle C\ \]

\[(углы\ равнобедренного\ \mathrm{\Delta}).\]

\[Следовательно:\ \]

\[ED = FD.\]

\[2)\ Так\ как\ ED = DF,\]

\[то\ \mathrm{\Delta}DEF - \ равнобедренный.\]

\[Что\ и\ требовалось\ доказать.\]