Решебник по геометрии 7 класс Атанасян ФГОС Задание 159

 

\[\boxed{\mathbf{159.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\ \]

\[\mathrm{\Delta}A_{1}B_{1}C_{1} - равнобедренные;\]

\[\angle ABC = \angle A_{1}B_{1}C_{1};\]

\[AB = A_{1}B_{1}.\]

\[\mathbf{Доказать:}\]

\[\mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1}.\]

\[\mathbf{Доказательство.}\]

\[1)\ По\ определению\ \]

\[равнобедренных\ \]

\[треугольников:\ \]

\[AB = BC;\ \ A_{1}B_{1} = B_{1}C_{1}.\]

\[Так\ как\ AB =\]

\[= A_{1}B_{1}(по\ условию):\]

\[AB = BC = A_{1}B_{1} = B_{1}C_{1}.\]

\[2)\ \mathrm{\Delta}ABC = \mathrm{\Delta}A_{1}B_{1}C_{1} - \ по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[\angle B = \angle B_{1}\ (по\ условию);\]

\[AB = A_{1}B_{1}\ (по\ условию);\]

\[BC = B_{1}C_{1}\ (см.\ пункт\ 1).\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{159.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

\[\mathrm{\Delta}ABC.\]

\[Построить:\]

\[\textbf{а)}\ биссектрису\ AK;\]

\[\textbf{б)}\ медиану\ BM;\]

\[\textbf{в)}\ высоту\ \text{CH.\ }\]

\[Построение.\]

\[\textbf{а)}\]

\[\textbf{б)}\ Разделим\ \text{CA}\ пополам.\]

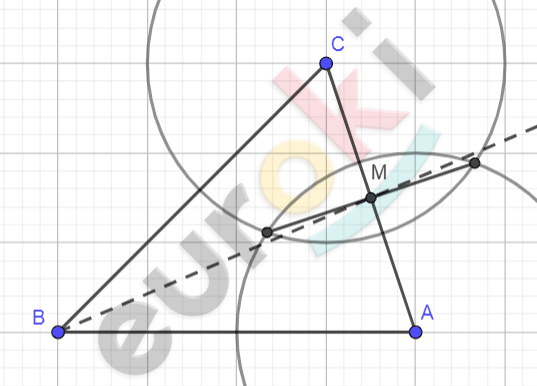
\[\textbf{в)}\ Сначала\ построим\ прямую\ a:\ \ \]

\[C \in a;\ \ a\bot AB.\]

\[Пересечение\ AB\ и\ \text{a\ }будет\ \]

\[точкой\ \text{H.}\]