Решебник по геометрии 7 класс Атанасян ФГОС Задание 152

 

\[\boxed{\mathbf{152.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Дано:\ \ \]

\[\angle AOB - тупой.\]

\[Построить:\]

\[луч\ \text{OX};\ \angle XOA = \angle XOB.\]

\[Построение.\]

\[1)\ Проведем\ окружность\ с\ \]

\[центром\ в\ точке\ O\ и\ \]

\[произвольным\ радиусом.\ \]

\[Получим\ точки\ ее\ пересечения\ \]

\[с\ углом\ AOB:M\ и\ \text{N.}\]

\[2)\ Проведем\ окружность\ с\ \]

\[центром\ в\ точке\ M;\ \ r = MN;\ \]

\[и\ окружность\ с\ центром\ в\ \]

\[точке\ N;\ \ r = MN.\]

\[Пересечением\ этих\ \]

\[окружностей\ будет\ точка\ K.\]

\[3)\ Через\ точки\ \text{O\ }и\ \text{K\ }проводим\ \]

\[луч\ \text{OX} - биссектрису\ угла\ AOB.\]

\[Получаем:\ \ \]

\[\angle AOX = \angle XOB;\ \ \angle AOX < 90{^\circ};\ \ \ \]

\[\angle XOB < 90{^\circ}.\]

\[\boxed{\mathbf{152.}\mathbf{еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

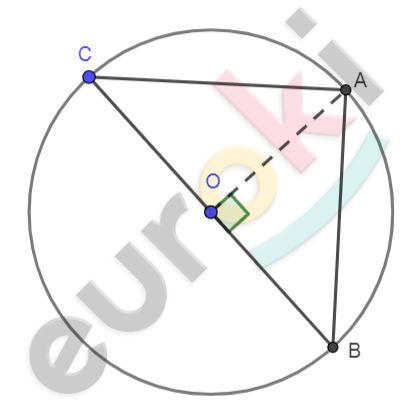
\[\mathbf{Дано:}\]

\[Окружность\ (O;r);\]

\[\text{BC} - диаметр;\]

\[\angle AOB = 90{^\circ}.\]

\[\mathbf{Доказать:}\]

\[AB = AC.\]

\[\mathbf{Доказательство.}\]

\[1)\ Мы\ получили\ \mathrm{\Delta}\text{ACO}\ и\ \mathrm{\Delta}ABO:\ \]

\[CO = OB = OA = r.\]

\[2)\ \mathrm{\Delta}\text{ACO} = \mathrm{\Delta}ABO - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[\angle AOB = \angle AOC = 90{^\circ}\ \]

\[(по\ условию);\]

\[AO - общая\ сторона;\]

\[CO = OB = r\ (см.\ пункт\ 1).\]

\[3)\ Отсюда\ получаем:\]

\[AC = AB.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]