Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 142
Задание 142
\[\boxed{\mathbf{142.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
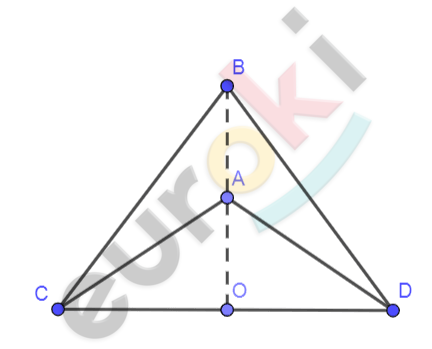
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}\text{ADC};\ \ \]
\[\mathrm{\Delta}\text{BCD} - равнобедренные;\]
\[AB \cap CD = O.\]
\[\mathbf{Доказать:}\]
\[\textbf{а)}\ \angle ADB = \angle ACB;\]
\[\textbf{б)}\ DO = OC.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}ADC - \ равнобедренный,\ \]
\[поэтому:\]
\[AC = AD;\ \ \]
\[\angle ACD = \angle ADC.\]
\[2)\ \mathrm{\Delta}BCD - равнобедренный,\ \]
\[поэтому:\]
\[CB = BD;\ \ \]
\[\angle BCD = \angle BDC.\]
\[3)\ Из\ первых\ двух\ пунктов\ \]
\[получаем:\]
\[\angle ADB = \angle BDC - \angle ADC;\]
\[\angle ACB = \angle BCD - \angle ACD.\]
\[Значит:\]
\[\angle ADB = \angle ACB.\]
\[4)\ \mathrm{\Delta}BCA = \mathrm{\Delta}\text{BDA} - \ по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[CB = BD;\ \ \]
\[CA = AD\ (по\ условию);\]
\[\angle ADB = \angle ACB\ (см.\ пункт\ 3).\]
\[Значит:\]
\[\ \angle CBO = \angle OBD.\]
\[5)\ \mathrm{\Delta}CBO = \mathrm{\Delta}OBD - \ по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[BO - общая\ сторона;\]
\[CB = BD - по\ условию;\]
\[\angle CBO = \angle OBD\ (см.\ пункт\ 4).\]
\[Следовательно:\]
\[CO = OD.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
\[\mathbf{Параграф\ }4\mathbf{.\ Задачи\ на\ построение}\]
\(\boxed{\mathbf{142.еуроки - ответы\ на\ пятёрку}}\)
\[\mathbf{Дано:}\]
\[⊿ABD;\ ⊿ADC;\]
\[AB = AC;\]
\[BD = DC;\]
\[\angle BAC = 50{^\circ}.\]
\[Найти:\]
\[\angle CAD.\]
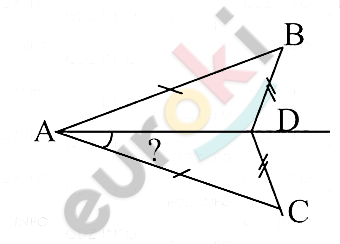
\[Решение.\]
\[1)\ ⊿ACD = ⊿ABD - по\ \]
\[третьему\ признаку:\]
\[AB = AC - по\ условию;\]
\[BD = DC - по\ условию;\]
\[AD - общая\ сторона.\]
\[Из\ равенства\ треугольников:\]
\[\angle BAD = \angle CAD.\]
\[2)\ \angle BAC = \angle BAD + \angle CAD =\]
\[= 2\angle CAD\]
\[2\angle CAD = \angle BAC\]
\[\angle CAD = 50{^\circ}\ :2\]
\[\angle CAD = 25{^\circ}.\]
\[Ответ:25{^\circ}.\ \]
