Решебник по геометрии 7 класс Атанасян ФГОС Задание 1411

\[\boxed{\mathbf{1411.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

\[движение\ g;\ \]

\[A\overset{g}{\rightarrow}B;\ \ B\overset{g}{\rightarrow}\text{A.}\]

\[Доказать:\]

\[g - центральная\ симметрия\ \]

\[или\ осевая\ симметрия.\]

\[Доказательство.\]

\[1)\ Если\ g - центральная\ \]

\[симметрия\ с\ центром\ \]

\[симметрии:\ \]

\[O\ и\ A\overset{o}{\rightarrow}B \Longrightarrow AO = OB.\ \]

\[Соответственно:\]

\[имеет\ указанное\ свойство.\]

\[2)\ Если\ g - осевая\ симметрия\ \]

\[с\ осью\ симметрии\ a\ и\ A\overset{a}{\rightarrow}A:\ \]

\[осевая\ симметрия\ также\ имеет\ \]

\[указанное\ свойство.\]

\[3)\ Пусть\ A\overset{g}{\rightarrow}B,\ B\overset{g}{\rightarrow}\text{A.\ }Возьмем\ \]

\[точку\ M\text{.\ }\]

\[Пусть\ при\ рассматриваемом\ \]

\[движении\ M\overset{g}{\rightarrow}\text{N.}\]

\[4)\ Расстояния\ должны\ \]

\[сохраняться:\]

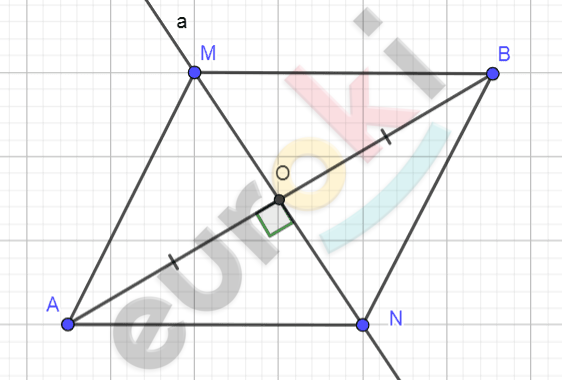
\[5)\ Отметим\ точку\ пересечения\ \]

\[диагоналей\ O = AB \cap MN:\]

\[AO = OB;\ \ MO = ON.\]

\[Если\ AM \neq BM \Longrightarrow \ g -\]

\[центральная\ симметрия\ \]

\[относительно\ точки\ \text{O.}\]

\[Если\ AM = BM \Longrightarrow \ AMBN -\]

\[ромб,\ MN\bot AB.\ \]

\[Можно\ по - прежнему\ \]

\[рассматривать\ g,как\ \]

\[центральную\ симметрию\ \]

\[относительно\ точки\ O.\]

\[Если\ M = N = O\ и\ AM = BM \Longrightarrow \ \]

\[\Longrightarrow g\ может\ быть\ \]

\[как\ центральной,\]

\[так\ и\ осевой\ симметрией.\]

\[Других\ возможностей\ нет.\]

\[Что\ и\ требовалось\ доказать.\]