Решебник по геометрии 7 класс Атанасян ФГОС Задание 1410

\[\boxed{\mathbf{1410.еуроки - ответы\ на\ пятёрку}}\]

\[Построить:\]

\[границу\ круга,\ площадь\ \]

\[которого\ равна\]

\[\textbf{а)}\ площади\ кольца\ между\ \]

\[двумя\ данными\ \]

\[концетрическими\ окружности;\]

\[\textbf{б)}\ площади\ данного\ полукруга;\]

\[\textbf{в)}\ площади\ данного\ \]

\[кругового\ сектора,\]

\[\ ограниченного\ дугой\ 60{^\circ}.\]

\[Построение.\]

\[\textbf{а)}\ S_{кольца} = \pi\left( R^{2} - r_{кольца}^{2} \right);\ \]

\[\ S_{круга} = \pi r_{круга}^{2};\]

\[\pi\left( R^{2} - r_{кольца}^{2} \right) = \pi r_{круга}^{2}.\]

\[Таким\ образом:\ \]

\[r_{круга}^{2} = \ R^{2} - r_{кольца}^{2} \Longrightarrow\]

\[\Longrightarrow что\ соответствует\ теореме\ \]

\[Пифагора.\]

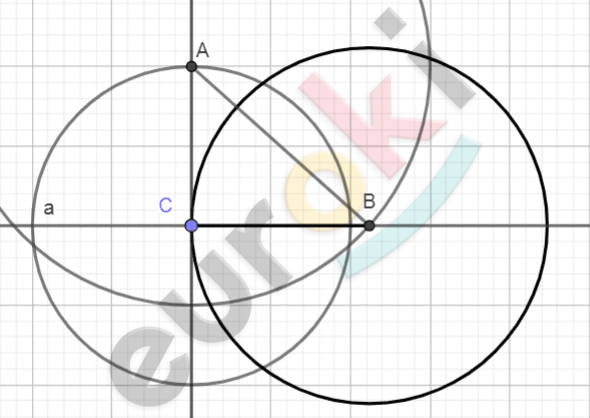
\[1)\ Построим\ прямую\ a\ и\ \]

\[отметим\ на\ ней\ точку\ C,\ \]

\[построим\ перпендикуляр\ \]

\[в\ точке\ \text{C\ }к\ прямой\ \text{a.}\]

\[2)\ Построим\ окружность\ \]

\[\left( C;r_{кольца} \right),\ отметим\ точку\ \text{A\ }\]

\[на\ пересечении\ \]

\[с\ перпендикуляром.\]

\[3)\ Построим\ окружность\ \]

\[(A;R),\ отметим\ точку\ \text{B\ }на\ \]

\[пересечении\ с\ прямой\ \text{a.}\]

\[4)\ Построим\ круг\ (B;BC) -\]

\[искомый.\]

\[\textbf{б)}\ S_{круга} = \pi r^{2};\ \ \ \]

\[S_{полуокружности} = \frac{\pi R^{2}}{2};\ \ \]

\[\pi r^{2} = \frac{\pi R^{2}}{2}.\]

\[Таким\ образом:\ \]

\[r = \frac{R}{\sqrt{2}} \Longrightarrow что\ \ соответствует\ \]

\[половине\ диагонали\ квадрата\]

\[со\ стороной\ \text{R.}\]

\[1)\ Отметим\ точку\ A\ на\ одном\ \]

\[из\ концов\ дуги\ \]

\[полуокружности.\]

\[2)\ Построим\ перпендикуляр\ \]

\[к\ отрезку\ \text{OA\ }через\ точку\ O,\ \]

\[отметим\ точку\ C\ на\ \]

\[пересечении\ \]

\[с\ полуокружностью.\]

\[3)\ Построим\ перпендикуляр\ \]

\[к\ отрезку\ \text{OA\ }через\ точку\ \text{A\ }и\ \]

\[перпендикуляр\ к\ прямой\ \text{OC\ }\]

\[через\ точку\ C,\ отметим\ \]

\[точку\ \text{B\ }на\ пересечении\ \]

\[перпендикуляров.\]

\[4)\ Отметим\ точку\ O_{1} -\]

\[пересечение\ диагоналей\ \]

\[квадрата\ \text{ABCO.}\]

\[5)\ Построим\ круг\ \left( O_{1};OO_{1} \right) -\]

\[искомый.\]

\[\textbf{в)}\ S_{круга} = \pi r^{2};\ \ \ \]

\[S_{сектора} = \frac{\pi R^{2}}{6};\ \ \]

\[\pi r^{2} = \frac{\pi R^{2}}{6}.\]

\[Таким\ образом:\ \]

\[r = \frac{R}{\sqrt{6}} \Longrightarrow что\ соответствует\ \]

\[половине\ диагонали\ квадрата\ \]

\[со\ стороной\ \text{R.}\]

\[1)\ Возьмем\ отрезок\ PQ -\]

\[как\ единичный.\]

\[2)\ Построим\ квадрат\ \]

\[со\ стороной\ PQ -\]

\[его\ диагональ\ равна\ \sqrt{2}.\]

\[3)\ Построим\ прямоугольный\ \]

\[треугольник\ с\ катетами\ \]

\[равными\ 2\ и\ \sqrt{2}\ с\ острыми\ \]

\[углами\ \text{A\ }и\ B - гипотенуза\ AB\ \]

\[равна\ \sqrt{6}.\]

\[4)\ Построим\ какой - нибудь\ \]

\[угол\ O_{1}.\]

\[5)\ На\ одной\ стороне\ угла\ O_{1}\ \]

\[отложим\ отрезки\ O_{1}B = AB\ и\ \]

\[O_{1}R = R;\]

\[на\ другой\ стороне\ O_{1}Q = PQ.\]

\[6)\ Через\ точку\ \text{R\ }проведем\ \]

\[прямую\ параллельную\ \text{BQ\ }и\ \]

\[отметим\ точку\ R_{1}\ \]

\[на\ пересечении\ со\ второй\ \]

\[стороной\ угла.\]

\[7)\ Построим\ круг\ \left( O_{1};O_{1}R_{1} \right) -\]

\[искомый.\]