Решебник по геометрии 7 класс Атанасян ФГОС Задание 1406

\[\boxed{\mathbf{1406.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

\[\mathrm{\Delta}ABC;\ \]

\[\angle A = a;\ \]

\[\angle B = 2a;\ \]

\[\angle C = 4a;\]

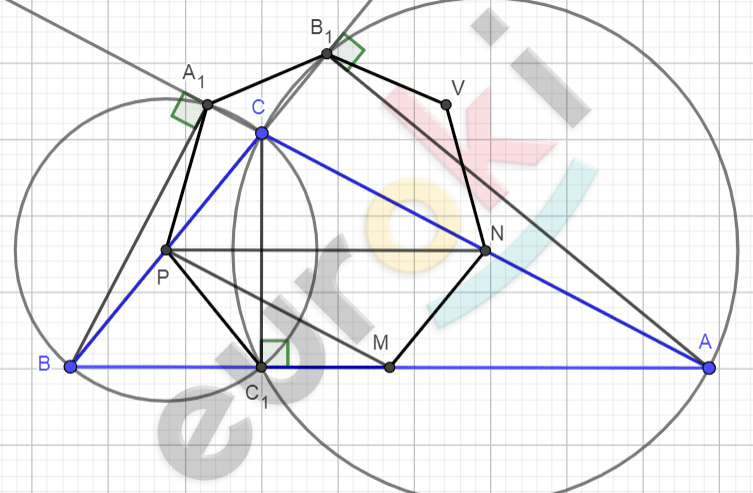
\[M,\ N,\ P - середины\ сторон;\ \]

\[AA_{1},\ BB_{1},\ CC_{1} - высота.\]

\[Доказать:\]

\[B_{1},\ A_{1},\ P_{1},\ C_{1},\ M,\ N - вершины\ \]

\[правильного\ 7 - угольника.\]

\[Доказательство.\]

\[1)\ \angle A + \angle B + \angle C = 180{^\circ}\]

\[\ a + 2a + 4a = 180{^\circ}.\]

\[\angle A = \frac{180{^\circ}}{7};\ \ \]

\[\angle B = 2 \cdot \frac{180{^\circ}}{7};\ \ \]

\[\angle C = 4 \cdot \frac{180{^\circ}}{7}.\]

\[2)\ Внутренний\ угол\ \]

\[правильного\ 7 - угольника:\ \]

\[\beta = 180{^\circ} - \frac{360{^\circ}}{7} = 5 \cdot \frac{180{^\circ}}{7}.\]

\[3)\ MN,\ PN,\ PM - средние\ \]

\[линии\ \mathrm{\Delta}ABC.\]

\[4)\ Четырехугольник\ BA_{1}CC_{1}\text{.\ \ \ }\]

\[\angle A_{1} = \angle C_{1} = 90^{0} \Longrightarrow вокруг\ \]

\[него\ можно\ описать\ \]

\[окружность\ диаметр\]

\[\ которой - отрезок\ BC,\]

\[центр - точка\ P:\ \]

\[PB = PC_{1} = PC = PA_{1} = \frac{1}{2}BC;\]

\[\angle C_{1}PA_{1} = 2\angle C_{1}BA_{1} =\]

\[= 2\left( 90^{0} - \angle A \right) = 5 \cdot \frac{180^{0}}{7} = \beta.\]

\[MN = \frac{1}{2}BC;\ \]

\[трапеция\ C_{1}PNM -\]

\[равнобедренная.\]

\[\angle PC_{1}M = \angle NMC_{1} =\]

\[= 180^{0} - \angle B = 5 \cdot \frac{180^{0}}{7} = \beta.\]

\[5)\ Четырехугольник\ AB_{1}CC_{1}\text{.\ }\]

\[\angle B_{1} = \angle C_{1} = 90^{0} \Longrightarrow вокруг\ \]

\[него\ можно\ \ описать\ \]

\[окружность,\ диаметр\ \]

\[которой - отрезок\ \text{AC},\ \]

\[центр - точка\ \text{N.}\]

\[NC_{1} = NC = NB_{1} = NA = \frac{1}{2}\text{AC.}\]

\[PM = \frac{1}{2}\text{AC.}\]

\[\mathrm{\Delta}B_{1}C_{1}N = \mathrm{\Delta}B_{1}\text{PN\ }по\ первому\ \]

\[признаку:\]

\[PB_{1} = NB = \frac{1}{2}AC;\]

\[\mathrm{\Delta}PA_{1}B_{1} = \mathrm{\Delta}NMC_{1};\]

\[\angle PA_{1}B_{1} = \beta;\]

\[A_{1}B_{1} = PA_{1} = \frac{1}{2}\text{BC.}\]

\[Таким\ образом,\ все\ отрезки,\ \]

\[последовательно\ \]

\[соединяющие\ исследуемые\ \]

\[шесть\ точек,\ равны\ \frac{\text{BC}}{2}.\ \]

\[Четыре\ угла\ между\ отрезками\ \]

\[равны\ внутреннему\ углу\ \]

\[правильного\ \]

\[7 - угольника:\ \]

\[5 \cdot 180^{0}\text{\ .\ }\]

\[Диагонали:\ \]

\[PB_{1} = BN = NC = PM = \frac{1}{2}\text{AC.}\]

\[Значит,\ исследуемые\ точки\ \]

\[являются\ шестью\ вершинами\ \]

\[из\ семи\ вершин\ правильного\ \]

\[7 - угольника.\]

\[Что\ и\ требовалось\ доказать.\]