Решебник по геометрии 7 класс Атанасян ФГОС Задание 1401

\[\boxed{\mathbf{1401.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

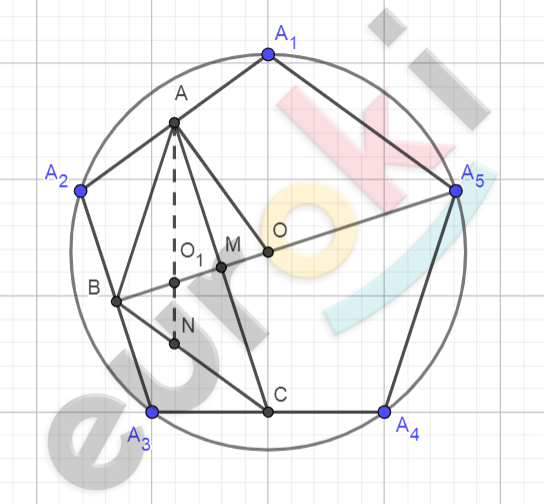
\[правильный\ пятиугольник\ \]

\[A_{1}A_{2}A_{3}A_{4}A_{5};\]

\[O(O,\ R) - описанная\ \]

\[окружность;\]

\[A,\ B,\ C - середины\ сторон\ \]

\[A_{1}A_{2};A_{2}A_{3}\ и\ A_{3}A_{4};\]

\[\ \left( O_{1},r \right) - вписанная\ в\ \mathrm{\Delta}ABC -\]

\[окружность.\]

\[Доказать:\]

\[осевая\ симметрия\ O\overset{\text{AC}}{\rightarrow}O_{1}.\]

\[Доказательство.\]

\[1)\ Обозначим\ сторону\ \]

\[пятиугольника\ A_{1}A_{2} = a.\]

\[\left. \ \begin{matrix} A_{2}A = A_{2}B = A_{3}B = A_{3}C = \frac{a}{2} \\ \angle AA_{2}B = \angle BA_{3}C = 108{^\circ}\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right\} \Longrightarrow\]

\[\Longrightarrow \mathrm{\Delta}AA_{2}B = \mathrm{\Delta}BA_{2}C \Longrightarrow\]

\[\Longrightarrow AB = BC.\]

\[2)\ \mathrm{\Delta}ABC - равнобедренный\ \]

\[с\ основанием\ AC:\]

\[\angle ABC = 180^{0} - 2\angle A_{2}BA =\]

\[= 180^{0} - \left( 180^{0} - 108^{0} \right) =\]

\[= 108^{0};\]

\[\angle BAC = \angle BCA =\]

\[= \frac{180^{0} - 108^{0}}{2} = 36^{0}.\]

\[3)\ Проведем\ отрезок\ BA_{5},\]

\[\ отметим\ точку\ пересечения\ \]

\[M = BA_{5} \cap AC.\]

\[4)\ \mathrm{\Delta}A_{2}A_{5}A_{3} - равнобедренный,\]

\[\ с\ основанием\ A_{2}A_{3}:\ \]

\[BA_{5} - медиана,\ биссектриса\ \]

\[и\ высота;\]

\[\text{BM} - медиана,\ биссектриса\ \]

\[и\ высота\ \mathrm{\Delta}ABC.\]

\[5)\ Оба\ центра\ окружностей\ \]

\[лежат\ на\ BA_{5}:\]

\[O \in BA_{5},\ O_{1} \in BA_{5}.\]

\[Через\ O_{1}\ подходит\ \]

\[биссектриса\ AN:\]

\[\angle O_{1}AC = \frac{\frac{1}{2}}{\text{BAC}} = 18^{0}.\]

\[\angle AOB = \angle A_{1}OA_{2} = \frac{360^{0}}{5} = 72^{0};\ \ \]

\[\angle AO_{1}M = 90^{0} - \angle O_{1}AC = 72^{0}.\]

\[6)\ \mathrm{\Delta}O_{1}AO - равнобедренный,\ \]

\[с\ основанием\ O_{1}O:\]

\[AM - медиана,биссектриса,\ \]

\[высота\ \overset{M \in AC}{\Rightarrow}AC - ось\ \]

\[симметрии.\]

\[Что\ и\ требовалось\ доказать.\]