Решебник по геометрии 7 класс Атанасян ФГОС Задание 1374

\[\boxed{\mathbf{1374.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\ \]

\[\mathrm{\Delta}ABC;\]

\[AA_{1},BB_{1},CC_{1} - биссектрисы\ \]

\[внешних\ углов;\]

\[AA_{1} \cap BC = A_{1};\]

\[BB_{1} \cap AC = B_{1};\]

\[CC_{1} \cap AB = C_{1}.\]

\[Доказать:\]

\[A_{1},B_{1},C_{1} - лежат\ на\ одной\ \]

\[прямой.\]

\[Доказательство.\]

\[1)\ Пусть\ BC = a;AC = b;\]

\[AB = c.\]

\[2)\ Единичные\ векторы\ \]

\[на\ сторонах\ \overrightarrow{i},\overrightarrow{j},\overrightarrow{k}:\ \]

\[\overrightarrow{\text{CB}} = a\overrightarrow{i};\overrightarrow{\text{CA}} = b\overrightarrow{j};\ \overrightarrow{\text{BA}} = c\overrightarrow{k}.\]

\[3)\ По\ теореме\ о\ биссектрисе\ \]

\[внешнего\ угла\ (задача\ 619):\]

\[\frac{CA_{1}}{A_{1}B} = \frac{\text{AC}}{\text{AB}}\]

\[\frac{CA_{1}}{CA_{1} - BC} = \frac{\text{AC}}{\text{AB}}\]

\[1 - \frac{\text{BC}}{CA_{1}} = \frac{\text{AB}}{\text{AC}}\]

\[\frac{a}{CA_{1}} = 1 - \frac{c}{b} = \frac{b - c}{b}\]

\[CA_{1} = \frac{\text{ab}}{b - c}.\]

\[Отсюда:\ \]

\[\overrightarrow{CA_{1}} = \frac{\text{ab}}{b - c}\overrightarrow{i}\ \left( так\ как\ \overrightarrow{CA_{1}} \uparrow \uparrow \overrightarrow{\text{CB}} \right).\]

\[4)\ Аналогично:\ \]

\[CB_{1} = \frac{\text{ab}}{a - c} \Longrightarrow \overrightarrow{CB_{1}} =\]

\[= \frac{\text{ab}}{a - c}\overrightarrow{j}\ \left( так\ как\ \overrightarrow{CB_{1}} \uparrow \uparrow \overrightarrow{\text{CA}} \right).\]

\[BC_{1} = \frac{\text{ac}}{a - b} \Longrightarrow \ \overrightarrow{BC_{1}} =\]

\[= \frac{\text{ac}}{a - b}\overrightarrow{k}\ \left( так\ как\ \overrightarrow{BC_{1}} \uparrow \uparrow \overrightarrow{\text{BA}} \right);\]

\[\overrightarrow{CC_{1}} = \overrightarrow{BC_{1}} - \overrightarrow{\text{BC}} = \frac{\text{ac}}{a - b}\overrightarrow{k} + a\overrightarrow{i};\]

\[\overrightarrow{\text{CB}} + \overrightarrow{\text{BA}} + \overrightarrow{\text{AC}} = \overrightarrow{0} \Longrightarrow\]

\[\Longrightarrow \ a\overrightarrow{i} - b\overrightarrow{j} + c\overrightarrow{k} = 0.\]

\[4)\ \left\{ \begin{matrix} k\overrightarrow{CA_{1}} + l\overrightarrow{CB_{1}} + m\overrightarrow{CC_{1}} = \overrightarrow{0} \\ k + l + m = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ }\]

\[Пусть\ m = 1:\]

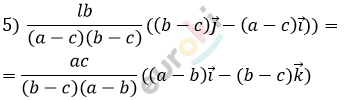
\[\frac{\text{lb}}{a - c}\left( - a\overrightarrow{i} + b\overrightarrow{j} + c\left( \overrightarrow{i} - \overrightarrow{j} \right) \right) =\]

\[= \frac{\text{ac}}{a - b}\left( a\overrightarrow{i} + c\overrightarrow{k} - b\left( \overrightarrow{i} + \overrightarrow{k} \right) \right)\]

\[\frac{\text{lbc}}{a - c}\left( \overrightarrow{k} - \overrightarrow{i} + \overrightarrow{j} \right) =\]

\[= \frac{\text{abc}}{a - b}\left( \overrightarrow{j} - \left( \overrightarrow{i} + \overrightarrow{k} \right) \right)\]

\[\frac{l}{a - c} = - \frac{a}{a - b}\]

\[\left\{ \begin{matrix} l = - \frac{a(a - c)}{a - b}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ l = - l - 1 = \frac{a(a - c)}{a - b} - 1 \\ \end{matrix} \right.\ \]

\[10)\ Таким\ образом:\ \]

\[k\overrightarrow{CA_{1}} + l\overrightarrow{CB_{1}} + m\overrightarrow{CC_{1}} = \overrightarrow{0}.\]

\[Значит:\]

\[точки\ A_{1},B_{1}\ и\ C_{1}\ лежат\ \]

\[на\ одной\ прямой\ (задача\ 907).\]

\[Что\ и\ требовалось\ доказать.\]