Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 136
Задание 136
\[\boxed{\mathbf{136.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:52.}\]
\[\mathbf{Дано:}\]
\[AB = AC;\]
\[BD = DC;\]
\[\angle\text{BAC} = 50{^\circ}.\]
\[\mathbf{Найти:}\]
\[\angle CAD = ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}ABD = \mathrm{\Delta}ACD - по\ трем\ \]
\[сторонам:\]
\[AD - общая\ сторона;\ \]
\[BD = DC(по\ условию);\]
\[AB = AC(по\ условию).\]
\[Значит:\]
\[\ \angle BAD = \angle DAC.\]
\[2)\ \angle BAC = \angle BAD + \angle DAC;\]
\[\angle BAD = \angle DAC\ (см.\ пункт\ 1):\]
\[\angle BAC = 2\angle CAD\ \]
\[50{^\circ} = 2\angle CAD\]
\[\angle CAD = 25{^\circ}.\]
\[Ответ:\ \angle CAD = 25{^\circ}.\]
\[\boxed{\mathbf{136.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ \mathbf{задачи:}\]
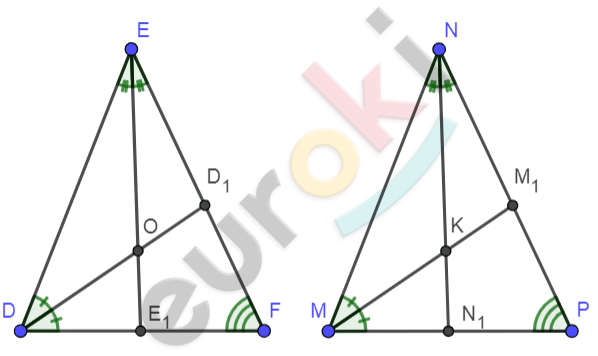
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}DEF;\ \mathrm{\Delta}MNP;\]
\[EF = NP;DF = MP;\]
\[\angle F = \angle P;\ \]
\[EE_{1} \cap DD_{1} = O;\]
\[EE_{1};DD_{1} - биссектрисы;\]
\[MM_{1} \cap NN_{1} = K;\]
\[MM_{1};\ NN_{1} - биссектрисы.\]
\[\mathbf{Доказать:}\]
\[\angle DOE = \angle MKN.\]
\[\mathbf{Доказательство.}\]
\[1)\ \mathrm{\Delta}\text{DEF} = \mathrm{\Delta}\text{MNP} - по\ двум\ \]
\[сторонам\ и\ углу\ между\ ними:\]
\[TF = NP\ (по\ условию);\ \]
\[DF = MP\ (по\ условию);\ \]
\[\angle F = \angle P\ (по\ условию).\]
\[Отсюда\ получаем:\]
\[DE = MN;\ \]
\[\angle D = \angle M;\]
\[\angle E = \angle N.\]
\[2)\ \angle EDO = \frac{1}{2}\angle D\ \]
\[\angle NMK = \frac{1}{2}\angle M\]
\[\angle D = \angle M\]
\[\angle EDO = \angle NMK.\]
\[\angle DEO = \frac{1}{2}\angle E\ \]
\[\angle MNK = \frac{1}{2}\angle N\ \]
\[\angle N = \angle E\ \]
\[\angle DEO = \angle MNK.\]
\[3)\ \ \mathrm{\Delta}DOE = \mathrm{\Delta}MKN - по\ стороне\ \]
\[и\ двум\ прилегающим\ к\ ней\ \]
\[углам:\ \]
\[DE = MN\ (см.\ пункт\ 1);\]
\[\angle EDO = \angle NMK\ \ (см.\ пункт\ 2);\]
\[\angle DEO = \angle MNK(см.\ пункт\ 2).\]
\[Следовательно:\]
\[\ \angle DOE = \angle MKN.\]
\[\mathbf{Что\ и\ требовалось\ доказать.}\]
