Решебник по геометрии 7 класс Атанасян ФГОС Задание 1315

\[\boxed{\mathbf{1315.еуроки - ответы\ на\ пятёрку}}\]

\[Дано:\]

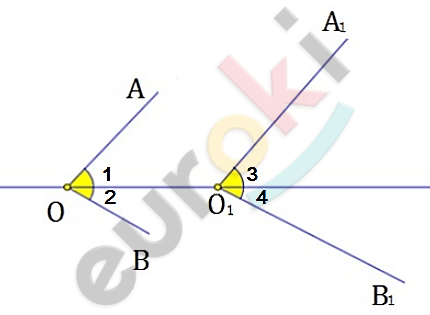
\[\angle AOB\sim\angle A_{1}O_{1}B_{1}.\]

\[Доказать:\]

\[\angle AOB = \angle A_{1}O_{1}B_{1}.\]

\[Доказательство.\]

\[При\ гомотетии\ прямая,\]

\[\ не\ проходящая\ через\ центр\ \]

\[гомотетии,переходит\ \]

\[в\ параллельную\ ей\ прямую:\]

\[OA \parallel O_{1}A_{1};\]

\[OB \parallel O_{1}B_{1}\text{.\ }\]

\[OA \parallel O_{1}A_{1};\ \ OO_{1} - секущая:\]

\[\angle 1 = \angle 3 -\]

\[как\ соответственные.\]

\[OB \parallel O_{1}B_{1};\ \ \ OO_{1} - секущая:\]

\[\angle 2 = \angle 4 -\]

\[как\ соответственные.\]

\[Так\ как:\]

\[\angle AOB = \angle 1 + \angle 2;\]

\[\angle A_{1}O_{1}B_{1} = \angle 3 + \angle 4.\]

\[Получаем:\]

\[\angle AOB = \angle A_{1}O_{1}B_{1}.\]

\[Что\ и\ требовалось\ доказать.\]