Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1256
Задание 1256
\[\boxed{\mathbf{1256.ОК\ ГДЗ - домашка\ н}а\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
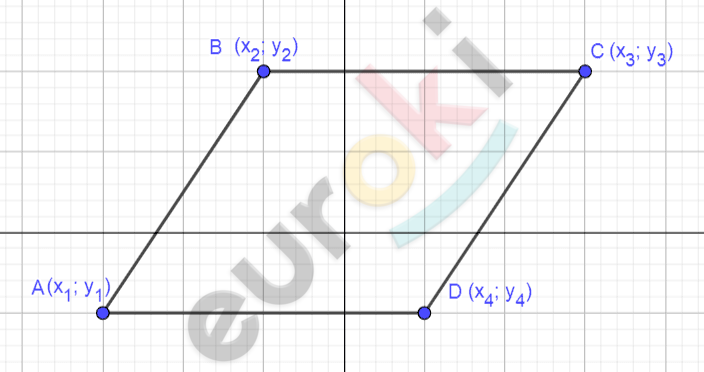
\[\textbf{а)}\ Дано:\]
\[четырехугольник\ ABCD;\]
\[A(x;y);\]
\[B\left( x_{2};y_{2} \right);\ \]
\[C\left( x_{3};y_{3} \right);\ \]
\[D\left( x_{4};y_{4} \right);\]
\[x_{1} + x_{3} = x_{2} + x_{4}\ и\ y_{1} + y_{3} =\]
\[= y_{2} + y_{4}.\]
\[Доказать:\]
\[ABCD - параллелограмм.\]
\[Доказательство:\]
\[\left. \ \begin{matrix} x_{1} + x_{3} = x_{2} + x_{4} \\ y_{1} + y_{3} = y_{2} + y_{4} \\ \end{matrix} \right\}\]
\[\left. \ \begin{matrix} x_{2} - x_{1} = x_{3} - x_{4} \\ y_{2} - y_{1} = y_{3} - y_{4} \\ \end{matrix} \right\}\]
\[\overrightarrow{\text{AB}}\left\{ x_{2} - x_{1};y_{2} - y_{1} \right\} =\]
\[= \overrightarrow{\text{DC}}\left\{ x_{3} - x_{4};y_{3} - y_{4} \right\}.\]
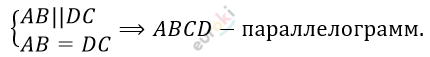
\[Что\ и\ требовалось\ доказать.\]
\[\textbf{б)}\ Дано:\]
\[четырехугольник\ ABCD;\ \]
\[A\left( x_{1};y_{1} \right);\ \]
\[B\left( x_{2};y_{2} \right);\]
\[C\left( x_{3};y_{3} \right);\]
\[D\left( x_{4};y_{4} \right);\]
\[ABCD - параллелограмм.\]
\[Доказать:\]
\[x_{1} + x_{3} = x_{2} + x_{4};\ \]
\[y_{1} + y_{3} = y_{2} + y_{4}.\]
\[Доказательство.\]
\[ABCD - параллелограмм:\]
\[\overrightarrow{\text{AB}}\left\{ x_{2} - x_{1};y_{2} - y_{1} \right\} =\]
\[= \overrightarrow{\text{DC}}\left\{ x_{3} - x_{4};y_{3} - y_{4} \right\};\]
\[\left\{ \begin{matrix} x_{2} - x_{1} = x_{3} - x_{4} \\ y_{2} - y_{1} = y_{3} - y_{4} \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x_{1} + x_{3} = x_{2} + x_{4} \\ y_{1} + y_{3} = y_{2} + y_{4} \\ \end{matrix} \right.\ \]
\[Что\ и\ требовалось\ доказать.\]
