Решебник по геометрии 7 класс Атанасян ФГОС Задание 123

 

\[\boxed{\mathbf{123.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

\[\mathbf{Дано:}\]

\[\angle A;\ \]

\[\ AD - биссектриса;\]

\[\angle ADB = \angle ADC.\]

\[\mathbf{Доказать:}\]

\[BD = CD.\]

\[\mathbf{Доказательство.}\]

\[1)\ \mathrm{\Delta}ABD = \mathrm{\Delta}ACD - по\ стороне\ \]

\[и\ двум\ прилежащим\ к\ ней\ \]

\[углам:\]

\[AD - общая\ сторона;\]

\[\angle BAD = \angle CAD\ \]

\[(AD - биссектриса\ по\ условию);\]

\[\angle BDA = \angle CDA\ (по\ условию).\]

\[2)\ Так\ как\ равные\ элементы\ в\ \]

\[равных\ фигурах\ равны:\]

\[BD = DC.\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]

\[\boxed{\mathbf{123.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\mathbf{\ задачи:}\]

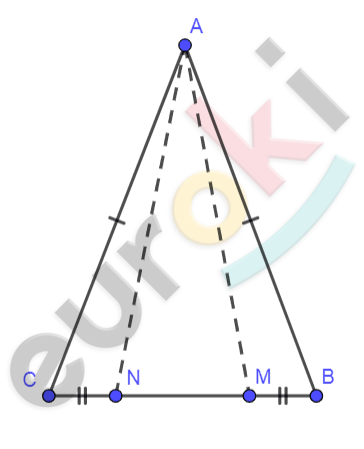
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равнобедренный;\]

\[AC = AB;\ \ \]

\[N \in BC;\]

\[BM = CN.\]

\[\mathbf{Доказать:}\]

\[\textbf{а)}\ \mathrm{\Delta}BAM = \mathrm{\Delta}CAN;\]

\[\textbf{б)}\ \mathrm{\Delta}AMN - равнобедренный.\]

\[\mathbf{Доказательство.}\]

\[\textbf{а)}\ \mathrm{\Delta}ACN\ и\ \mathrm{\Delta}ABM\ равны\ \]

\[по\ 2\ сторонам\ и\ углу\ между\ \]

\[ними:\]

\[CN = MB(по\ условию);\ \ \]

\[AC = AB(\ по\ условию);\]

\[\angle C = \angle B\ \]

\[(\ \mathrm{\Delta}ABC - равнобедренный).\]

\[Получаем:\]

\[AN = AM.\]

\[\textbf{б)}\ \mathrm{\Delta}AMN - равнобедренный,\ \]

\[так\ как:\]

\[AN = AM\ (см.\ пункт\ а).\]

\[\mathbf{Что\ и\ требовалось\ доказать.}\]