Решебник по геометрии 7 класс Атанасян ФГОС Задание 1137

 

\[\boxed{\mathbf{1137.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[n = 2\ оборота;\]

\[C_{n} = 84\ 152\ км;\]

\[R_{3} = 6\ 370\ км.\]

\[\mathbf{Найти:}\]

\[h - ?\]

\[\mathbf{Решение.}\]

\[1)\ Длина\ одного\ оборота:\]

\[C_{1} = \frac{84\ 152}{2} = 42\ 076\ км.\]

\[2)\ C = 2\pi R\]

\[R_{орбиты} = \frac{S}{2\pi} = \frac{42\ 076}{2 \bullet 3,14} =\]

\[= 6\ 700\ км.\]

\[3)\ R_{орбиты} = R_{3} + h\]

\[h = R_{орбиты} - R_{земли}\]

\[h = 6\ 700 - 6\ 370 = 330\ км.\]

\[Ответ:космический\ корабль\ \]

\[находится\ в\ 330\ км\ над\ землей.\]

\[\boxed{\mathbf{1137.еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[A(2;8);\]

\[B( - 1;5);\]

\[C(3;1).\]

\[\mathbf{Найти:}\]

\[\cos{\angle A;}\]

\[\cos{\angle B;}\]

\[\cos{\angle C}.\]

\[\mathbf{Решение.}\]

\[1)\ AB = \sqrt{(2 + 1)^{2} + (8 - 5)^{2}} =\]

\[= \sqrt{9 + 9} = 3\sqrt{2};\]

\[BC = \sqrt{(3 + 1)^{2} + (1 - 5)^{2}} =\]

\[= \sqrt{16 + 16} = 4\sqrt{2};\]

\[AC = \sqrt{(3 - 2)^{2} + (1 - 8)^{2}} =\]

\[= \sqrt{1 + 49} = 5\sqrt{2}.\]

\[2)\ По\ теореме\ косинусов:\]

\[32 = 18 + 50 - 60 \bullet \cos{\angle A}\]

\[60 \bullet \cos{\angle A} = 36\]

\[\cos{\angle A} = \frac{36}{60} = \frac{3}{5} = 0,6.\]

\[50 = 18 + 32 - 48 \bullet \cos{\angle B}\]

\[{48 \bullet cos}{\angle B} = 0\]

\[\cos{\angle B = 0}.\]

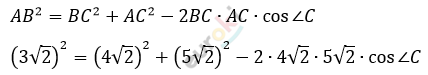
\[18 = 32 + 50 - 80 \bullet \cos{\angle C}\]

\[80 \bullet \cos{\angle A} = 64\]

\[\cos{\angle C} = \frac{64}{80} = \frac{8}{10} = 0,8.\]

\[\mathbf{Ответ:}\cos{\angle A} = 0,6;\]

\[\cos{\angle B} = 0;\cos{\angle C = 0,8}\mathbf{.}\]