Решебник по геометрии 7 класс Атанасян ФГОС Задание 1122

 

\[\boxed{\mathbf{1122.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[R = 3\ м;\]

\[r = 1\ м;\]

\[1\ м^{2}\ дороги = 0,8\ дм^{3}\ песка.\]

\[\mathbf{Найти:}\]

\[объем\ песка - ?\]

\[\mathbf{Решение.}\]

\[1)\ S_{кл} = \pi R^{2} = \pi \bullet 3^{2} = 9\pi\ м^{2}.\]

\[2)\ S_{кл + дор} = \pi \bullet (R + r)^{2} =\]

\[= \pi \bullet 4^{2} = 16\ \pi\ м^{2}.\]

\[3)\ S_{дороги} = S_{кл + дор} - S_{кл} =\]

\[= 15\pi - 9\pi = 7\pi\ м^{2}.\]

\[4)\ V_{песка} = 7\pi \bullet 0,8 = 5,6\pi =\]

\[= 5,6 \bullet 3,14 = 17,6\ дм^{3}.\]

\[Ответ:необходимо\ 17,6\ дм^{3}\ \]

\[песка\ для\ посыпки\ дороги.\]

\[\boxed{\mathbf{1122.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ \ задачи:\]

\[\mathbf{Дано:}\]

\[Окружность\ (O;r);\]

\[\mathrm{\Delta}ABC\ и\ \mathrm{\Delta}A_{1}\text{BC.}\]

\[\mathbf{Доказать:}\]

\[\frac{\text{BC}}{\sin{\angle A}} = 2R.\]

\[\mathbf{Доказательство.}\]

\[1)\ Пусть\ R - радиус\ описанной\]

\[\ вокруг\ \mathrm{\Delta}ABC\ окружности.\]

\[2)\ Проведем\ BA_{1} =\]

\[= \text{d\ }и\ рассмотрим\ \mathrm{\Delta}A_{1}BC:\]

\[\angle A_{1}CB = 90{^\circ} \Longrightarrow BC =\]

\[= BA_{1} \bullet \sin{\angle A_{1}}.\]

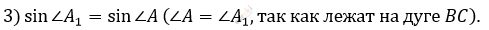
\[4)\ BC = BA_{1}\sin{\angle A}\]

\[BC = 2R \bullet \sin{\angle A} = \frac{\text{BC}}{\sin{\angle A}} = 2R.\]

\[Что\ и\ требовалось\ доказать.\]