Решебник по геометрии 7 класс Атанасян ФГОС Задание 1119

 

\[\boxed{\mathbf{1119.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[c_{арены} = 41\ м.\]

\[\mathbf{Найти:}\]

\[d - ?\]

\[\ S_{арены} - ?\]

\[\mathbf{Решение.}\]

\[1)\ C = 2\pi R\]

\[R = \frac{C}{2\pi} = \frac{41}{2 \bullet 3,14} = 6,53\ м.\]

\[2)\ d = 2R = 2 \bullet 6,53 = 13,06\ м.\]

\[3)\ S = \pi R^{2} = 3,14 \bullet {6,53}^{2} =\]

\[= 133,89\ м^{2}.\]

\[Ответ:d = 13,06\ м;\]

\[S = 133,89\ м^{2}.\]

\[\boxed{\mathbf{1119.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

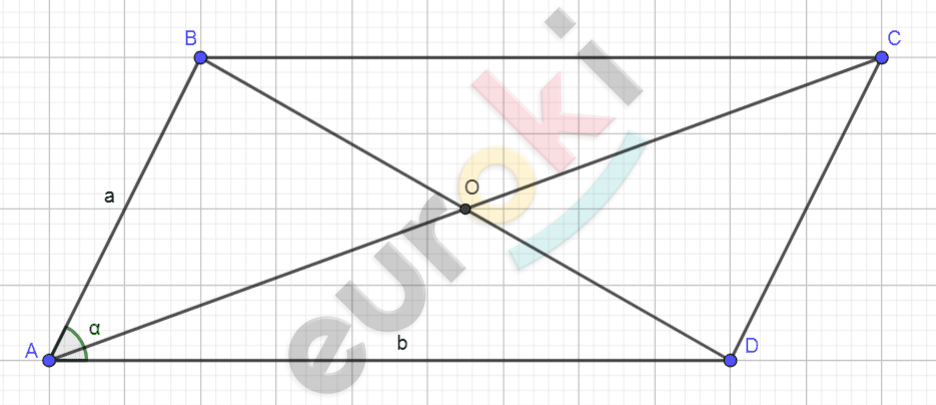
\[\mathbf{Дано:}\]

\[ABCD - параллелограмм;\]

\[AD = b;\]

\[\angle A = \alpha;\]

\[AB = a.\]

\[\mathbf{Найти:}\]

\[BD - ?\]

\[AC - ?\]

\[\angle AOB - ?\]

\[\mathbf{Решение.}\]

\[1)\ По\ теореме\ косинусов:\]

\[BD^{2} = a^{2} + b^{2} - 2ab \bullet \cos\alpha\]

\[BD = \sqrt{a^{2} + b^{2} - 2ab \bullet \cos\alpha}.\]

\[AC^{2} =\]

\[= a^{2} + b^{2} - 2ab \bullet \cos{(180{^\circ} - \alpha)}\]

\[AC = \sqrt{a^{2} + b^{2} + 2ab \bullet \cos\alpha}.\]

\[2)\ Рассмотрим\ \mathrm{\Delta}ABO:\]

\[BO = \frac{\text{BD}}{2} =\]

\[= \frac{\sqrt{a^{2} + b^{2} - 2ab \bullet \cos\alpha}}{2};\]

\[AO = \frac{\text{AC}}{2} =\]

\[= \frac{\sqrt{a^{2} + b^{2} + 2ab \bullet \cos\alpha}}{2}.\]

\[По\ теореме\ косинусов:\]