Решебник по геометрии 7 класс Атанасян ФГОС Задание 1062

 

\[\boxed{\mathbf{1062.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}DEF;\]

\[DE = 4,5\ дм;\]

\[EF = 9,9\ дм;\]

\[DF = 70\ см.\]

\[\mathbf{Найти:}\]

\[\angle D;\angle E\ и\ \angle F.\]

\[\mathbf{Решение.}\]

\[1)\ DE = 4,5\ дм = 45\ см;\]

\[EF = 9,9\ дм = 99\ см.\]

\[2)\ По\ теореме\ косинусов:\]

\[EF^{2} =\]

\[= DE^{2} + DF^{2} - 2DE \bullet DF \bullet \cos{\angle D};\]

\[9801 =\]

\[= 2025 + 4900 - 6300 \bullet \cos{\angle D}\]

\[2876 = - 6300\cos{\angle D}\]

\[\cos{\angle D} = - 0,4565\]

\[\angle D = 117{^\circ}10^{'}.\]

\[3)\ По\ теореме\ синусов:\]

\[\frac{\text{DE}}{\sin{\angle F}} = \frac{\text{EF}}{\sin{\angle D}} = \frac{\text{DF}}{\sin{\angle E}};\]

\[\frac{99}{\sin{117{^\circ}10^{'}}} = \frac{45}{\sin{\angle F}}\]

\[\sin{\angle F} = \frac{45 \bullet 0,8897}{99} = 0,4044\]

\[\angle F = 23{^\circ}51^{'}.\]

\[4)\ \angle E =\]

\[= 180{^\circ} - \left( 23{^\circ}51^{'} + 117{^\circ}10^{'} \right) =\]

\[= 38{^\circ}59^{'}.\]

\[Ответ:\ \angle D = 117{^\circ}10^{'};\ \]

\[\angle E = 38{^\circ}59^{'};\ \angle F = 23{^\circ}51'.\]

\[\boxed{\mathbf{1062.еуроки - ответы\ на\ пятёрку}}\]

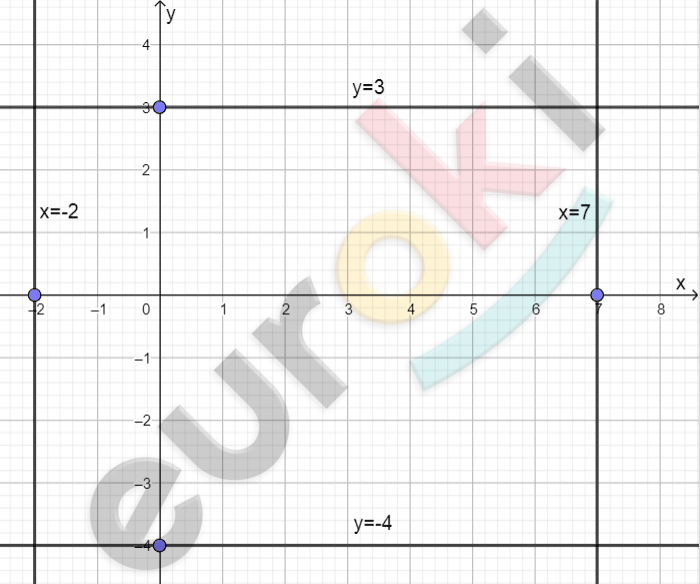
\[\mathbf{а})\ y = 3;\]

\[\textbf{б)}\ x = - 2;\]

\[\textbf{в)}\ y = - 4;\]

\[\textbf{г)}\ x = 7.\]