Решебник по геометрии 7 класс Атанасян ФГОС Задание 1042

 

\[\boxed{\mathbf{1042.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ задачи:\]

\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC - равносторон;\]

\[AB = a;\]

\[BD\bot AC.\]

\[\mathbf{Найти:}\]

\[скалярное\ произведение\ \]

\[векторов.\]

\[\mathbf{Решение.}\]

\[1)\ \mathrm{\Delta}ABC - равносторонний:\ \]

\[\angle A = \angle B = \angle C =\]

\[= 60{^\circ}\ (по\ свойству).\]

\[2)\ BD\bot AC \Longrightarrow \angle ADB = 90{^\circ}.\]

\[\textbf{а)}\ \overrightarrow{\text{AB}} \bullet \overrightarrow{\text{AC}} = a \bullet a \bullet \cos{60{^\circ}} =\]

\[= a^{2} \bullet \frac{1}{2} = \frac{a^{2}}{2};\]

\[\textbf{б)}\ \overrightarrow{\text{AC}} \bullet \overrightarrow{\text{CB}} = a \bullet a \bullet \cos{120{^\circ}} =\]

\[= a^{2} \bullet \left( - \frac{1}{2} \right) = - \frac{a^{2}}{2};\]

\[\textbf{в)}\ \overrightarrow{\text{AC}} \bullet \overrightarrow{\text{BD}} =\]

\[= \left| \overrightarrow{\text{AC}} \right| \bullet \left| \overrightarrow{\text{BD}} \right| \bullet \cos{90{^\circ}} = 0;\]

\[\textbf{г)}\ \overrightarrow{\text{AC}} \bullet \overrightarrow{\text{AC}} = a \bullet a \bullet \cos{0{^\circ}} =\]

\[= a^{2} \bullet 1 = a^{2}.\]

\[\boxed{\mathbf{1042.еуроки - ответы\ на\ пятёрку}}\]

\[Рисунок\ по\ условию\ задачи:\]

\[Сформулируем\ обратное\ \]

\[утверждение:\]

\[если\ диагонали\ трапеции\ \]

\[равны\ (то\ есть\ BD = AC),\ то\ \]

\[трапеция\ равнобедренная.\]

\[Рисунок\ по\ условию\ обратной\ \]

\[задачи:\]

\[\mathbf{Дано:}\]

\[\textbf{а)}\ ABCD - равнобедренная\ \]

\[трапеция;\]

\[\textbf{б)}\ BD = AC.\]

\[\mathbf{Доказать:}\]

\[\textbf{а)}\ BD = AC;\]

\[\textbf{б)}\ ABCD - равнобедренная\ \]

\[трапеция.\]

\[\mathbf{Доказательство.}\]

\[\textbf{а)}\ 1)\ Прямоугольная\ система\ \]

\[координат:\]

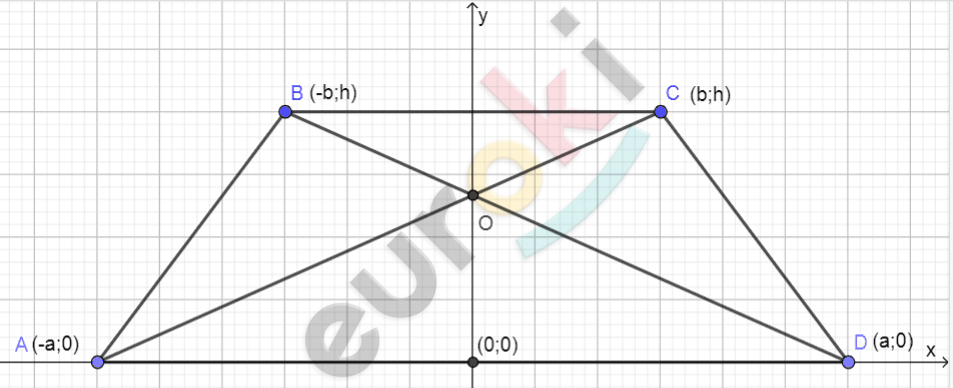
\[A( - a;0);D(a;0);B( - b;h);\]

\[C(b;h);\]

\[\left( OY - ось\ симметрии\ \text{ABCD} \right).\]

\[2)\ BD = \sqrt{(a + b)^{2} + (0 - h)^{2}} =\]

\[= \sqrt{(a + b)^{2} + h^{2}};\]

\[AC = \sqrt{(b + a)^{2} + (h - 0)^{2}} =\]

\[= \sqrt{(a + b)^{2} + h^{2}};\]

\[BD = AC.\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ 1)\ Прямоугольная\ система\ \]

\[координат:\]

\[A( - a;0);D(a;0);B(b;h);\]

\[C(с;h).\]

\[2)\ AC = BD\ (по\ условию) \Longrightarrow\]

\[\Longrightarrow AC^{2} = BD^{2}:\]

\[AC = \sqrt{(c + a)^{2} + (h - 0)^{2}} =\]

\[= \sqrt{(c + a)^{2} + h^{2}}\]

\[AC^{2} = (c + a)^{2} + h^{2};\]

\[BD = \sqrt{(a - b)^{2} + (0 - h)^{2}} =\]

\[= \sqrt{(a - b)^{2} + h^{2}}\]

\[BD^{2} = (a - b)^{2} + h^{2}.\]

\[3)\ (c + a)^{2} + h^{2} = (a - b)^{2} + h^{2}\]

\[(c + a)^{2} = (a - b)^{2}\]

\[(c + a)^{2} - (a - b)^{2} = 0\]

\[(c + a - a + b)(c + a + a - b) =\]

\[= 0\]

\[(c + b)(2a + c - b) = 0\]

\[a > 0;b < c \Longrightarrow\]

\[2a + c - b > 0\]

\[c + b = 0 \Longrightarrow b = - c \Longrightarrow\]

\[\Longrightarrow B( - c;h).\]

\[4)\ AB =\]

\[= \sqrt{( - c + a)^{2} + (h - 0)^{2}} =\]

\[= \sqrt{(a - c)^{2} + h^{2}};\]

\[CD = \sqrt{(a - c)^{2} + (0 - h)^{2}} =\]

\[= \sqrt{(a - c)^{2} + h^{2}};\]

\[AB = CD \Longrightarrow ABCD -\]

\[равнобедренная\ трапеция.\ \]

\[Что\ и\ требовалось\ доказать.\]