Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 7 класс Атанасян ФГОС Задание 1034
Задание 1034
\[\boxed{\mathbf{1034.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
\[\mathbf{Дано:}\]
\[ABCD - равнобедренная\ \]
\[трапеция;\ \]
\[AB = CD = BC;\]
\[AD = 10\ см;\]
\[\angle A = \angle D = 70{^\circ}.\]
\[\mathbf{Найти:}\]
\[P_{\text{ABCD}} - ?\]
\[\mathbf{Решение.}\]
\[1)\ Пусть\ AB = x:\]
\[\ AB_{1} = C_{1}D = \frac{10 - x}{2}.\]
\[2)\ В\ \mathrm{\Delta}\text{AB}B_{1}:\]
\[\cos{70{^\circ}} = \frac{AB_{1}}{\text{AB}}\]
\[0,342 = \frac{10 - x}{2} \bullet \frac{1}{x}\]
\[0,684x = 10 - x\]
\[1,684x = 10\]
\[x = 5,94 \approx 6\ см.\]
\[3)\ P_{\text{ABCD}} =\]
\[= AB + BC + CD + AD =\]
\[= 6 \bullet 3 + 10 = 28\ см.\]
\(Ответ:28\ см.\)
\[\boxed{\mathbf{1034.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\ задачи:\]
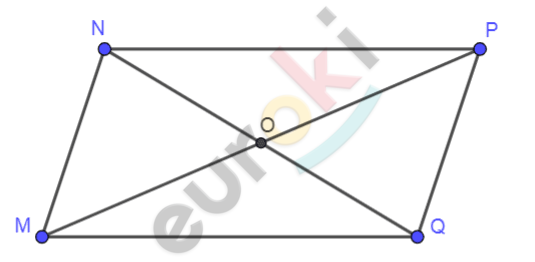
\[\mathbf{Дано:}\]
\[MNPQ - четырехугольник;\]
\[\textbf{а)}\ M(1;1);\]
\[N(6;1);\]
\[P(7;4);\]
\[Q(2;4).\]
\[\textbf{б)}\ M( - 5;1);\]
\[N( - 4;4);\]
\[P( - 1;5);\]
\[Q( - 2;2).\]
\[\mathbf{Доказать:}\]
\[MNPQ - параллелограмм.\]
\[Найти:\]
\[MN\ и\ \text{PQ.}\]
\[\mathbf{Решение.}\]
\[\textbf{а)}\ 1)\ MQ =\]
\[= \sqrt{(2 - 1)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{1 + 9} = \sqrt{10}\]
\[NP = \sqrt{(7 - 6)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{1 + 9} = \sqrt{10}\]
\[MN = \sqrt{(6 - 1)^{2} + (1 - 1)^{2}} =\]
\[= \sqrt{25 + 0} = 5\]
\[PQ = \sqrt{(2 - 7)^{2} + (4 - 4)^{2}} =\]
\[= \sqrt{25 + 0} = 5\]
\[3)\ NQ = \sqrt{(2 - 6)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{16 + 9} = 5;\]
\[MP = \sqrt{(7 - 1)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{36 + 9} = \sqrt{45} = 3\sqrt{5}.\]
\[\textbf{б)}\ 1)\ MQ =\]
\[= \sqrt{( - 2 + 5)^{2} + (2 - 1)^{2}} =\]
\[= \sqrt{9 + 1} = \sqrt{10}\]
\[NP = \sqrt{( - 1 + 4)^{2} + (5 - 4)^{2}} =\]
\[= \sqrt{9 + 1} = \sqrt{10}\]
\[MN = \sqrt{( - 4 + 5)^{2} + (4 - 1)^{2}} =\]
\[= \sqrt{1 + 9} = \sqrt{10}\]
\[PQ = \sqrt{( - 2 + 1)^{2} + (2 - 5)^{2}} =\]
\[= \sqrt{1 + 9} = \sqrt{10}\]
\[3)\ NQ =\]
\[= \sqrt{( - 2 + 4)^{2} + (2 - 4)^{2}} =\]
\[= \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2};\]
\[MP = \sqrt{( - 1 + 5)^{2} + (5 - 1)^{2}} =\]
\[= \sqrt{16 + 16} = 4\sqrt{2}.\]
\[\mathbf{Ответ:}\mathbf{\ }а)\ NQ = 5;MP = 3\sqrt{2};\ \]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ б)\ NQ = 2\sqrt{2};MP = 4\sqrt{2}.\]
