Решебник по геометрии 7 класс Атанасян ФГОС Вопросы для повторения к главе XI

\[\boxed{\mathbf{Вопросы\ для\ повторения\ к\ главе\ }\mathbf{\text{XI}}\mathbf{.еуроки - ответы\ на\ пятёрку}}\]

\[\boxed{\mathbf{1.}}\]

\[Лемма:\]

\[если\ векторы\ \overrightarrow{a}\ и\ \overrightarrow{b}\ \]

\[коллинеарны\ и\ \overrightarrow{a} \neq \overrightarrow{0},\ то\ \]

\[существует\ такое\ число\ k,\ \]

\[что\ \overrightarrow{b} = k\overrightarrow{a}.\]

\[Доказательство.\]

\[Случай\ 1:\ \ \ \overrightarrow{a} \uparrow \uparrow \overrightarrow{b}.\]

\[Пусть\ k = \frac{\left| \overrightarrow{b} \right|}{\left| \overrightarrow{a} \right|};\ \ k \geq 0:\]

\[векторы\ k\overrightarrow{a}\ и\ \overrightarrow{b} -\]

\[сонаправлены.\]

\[Их\ длины\ равны:\]

\[\left| k\overrightarrow{a} \right| = |k| \cdot \left| \overrightarrow{a} \right| = \frac{\left| \overrightarrow{b} \right|}{\left| \overrightarrow{a} \right|} \cdot \left| \overrightarrow{a} \right| = \left| \overrightarrow{b} \right|.\]

\[Отсюда:\]

\[\overrightarrow{b} = k\overrightarrow{a}.\]

\[Случай\ 2:\ \ \overrightarrow{a} \uparrow \downarrow \overrightarrow{b}.\]

\[Пусть\ k = - \frac{\left| \overrightarrow{b} \right|}{\left| \overrightarrow{a} \right|};\ \ k < 0:\]

\[векторы\ k\overrightarrow{a}\ и\ \overrightarrow{b} -\]

\[сонаправлены.\]

\[Их\ длины\ равны:\]

\[\left| k\overrightarrow{a} \right| = |k| \cdot \left| \overrightarrow{a} \right| = \frac{\left| \overrightarrow{b} \right|}{\left| \overrightarrow{a} \right|} \cdot \left| \overrightarrow{a} \right| = \left| \overrightarrow{b} \right|.\]

\[Отсюда:\]

\[\overrightarrow{b} = k\overrightarrow{a}.\]

\[Лемма\ доказана.\]

\[\boxed{\mathbf{2.}}\]

\[Пусть\ \overrightarrow{a}\ и\ \overrightarrow{b} - два\ данных\ \]

\[вектора.\]

\[Если\ вектор\ \overrightarrow{p} = x\overrightarrow{a} + y\overrightarrow{b};\ \ \]

\[x\ и\ y - некоторые\ числа:\]

\[вектор\ \overrightarrow{p}\ разложен\ \]

\[по\ векторам\ \overrightarrow{a}\ и\ \overrightarrow{b};\]

\[числа\ \text{x\ }и\ \text{y\ }называются\ \]

\[коэффициентами\ разложения.\]

\[\boxed{\mathbf{3.}}\]

\[\mathbf{Теорема:}\]

\[на\ \ плоскости\ \ любой\ \ вектор\ \ \]

\[можно\ \ разложить\ по\ \ двум\ \ \]

\[данным\ неколлинеарным\ \ \]

\[векторам,\ причём\ \]

\[коэффициенты\ \ разложения\ \]

\[определяются\ \ единственным\ \ \]

\[образом.\]

\[Доказательство.\]

\[Пусть\ \overrightarrow{a}\ \ \ и\ \ \overrightarrow{b}\ \ - данные\ \]

\[неколлинеарные\ векторы.\ \]

\[Докажем\ сначала,\ что\ любой\ \]

\[вектор\ можно\ разложить\ \]

\[по\ векторам\ \overrightarrow{a}\ \ и\ \ \overrightarrow{b}\text{.\ }\]

\[Возможны\ два\ случая:\ \]

\[1)\ Вектор\ \overrightarrow{p}\ коллинеарен\ \]

\[одному\ из\ векторов,\ например\ \]

\[вектору\ \overrightarrow{b}.\]

\[По\ лемме\ о\ коллинеарных\ \]

\[векторах:\]

\[\overrightarrow{p} = 0 \cdot \overrightarrow{a} + y \cdot \overrightarrow{b} - то\ есть\ \]

\[вектор\ \overrightarrow{p}\ разложен\ \]

\[по\ векторам\ \overrightarrow{a}\ и\ \overrightarrow{b}.\]

\[2)\ Вектор\ \overrightarrow{p}\ не\ коллинеарен\ \]

\[ни\ одному\ из\ векторов.\]

\[Отметим\ какую - нибудь\ \]

\[точку\ \text{O\ }и\ отложим\ от\ \ нее\ \]

\[векторы\ \]

\[\overrightarrow{\text{OA}} = \overrightarrow{a};\ \ \overrightarrow{\text{OB}} = \overrightarrow{b};\ \ \overrightarrow{\text{OP}} = \overrightarrow{p}.\]

\[Через\ точку\ \text{P\ }проведем\ \]

\[прямую\ OD \parallel OB.\]

\[По\ правилу\ треугольника:\]

\[\overrightarrow{p} = \overrightarrow{\text{OD}} + \overrightarrow{\text{DP}} = x\overrightarrow{a} + y\overrightarrow{b}.\]

\[Докажем\ теперь,\ что\ \]

\[коэффициенты\ x\ и\ y\ \]

\[разложения\ определяются\ \]

\[единственным\ образом.\]

\[Допустим,\ что\ существует\ еще\ \]

\[разложение:\]

\[\overrightarrow{p} = x_{1}\overrightarrow{a} + x_{2}\overrightarrow{b}.\]

\[Вычтем\ второе\ равенство\ \]

\[из\ первого,\ используя\ правила\ \]

\[действий\ над\ векторами,\ \]

\[получим:\ \]

\[\overrightarrow{0} = \left( x - x_{1} \right)\overrightarrow{a} + \left( x - x_{2} \right)\overrightarrow{b}.\]

\[Это\ равенство\ выполняется\ \]

\[при:\]

\[x - x_{1} = 0;\ \ \ \ \ x - x_{2} = 0\]

\[x = x_{1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ x = x_{2}.\]

\[Значит,\ коэффициенты\ \]

\[разложения\ вектора\ \overrightarrow{p}\ \]

\[определяются\ единственным\ \]

\[образом.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{4.}}\]

\(\mathbf{Для\ \ задания\ \ прямоугольной\ \ }\)

\[\mathbf{системы\ \ координат\ \ нужно\ \ }\]

\[\mathbf{провести\ }\mathbf{две\ \ взаимно\ }\mathbf{\ }\]

\[\mathbf{перпендикулярные\ \ прямые,\ }\]

\[\mathbf{на\ \ каждой\ из\ \ них\ \ выбрать\ }\mathbf{\ }\]

\[\mathbf{направление\ \ }\]

\[\left( \mathbf{оно\ \ обозначается\ стрелкой} \right)\mathbf{\ }\]

\[\mathbf{и\ \ выбрать\ \ единицу\ \ }\]

\[\mathbf{измерения\ \ отрезков.}\]

\[\mathbf{При\ выбранной\ единице\ }\]

\[\mathbf{измерения\ отрезков\ длина\ \ }\]

\[\mathbf{каждого\ \ отрезка\ \ }\mathbf{выражается\ \ }\]

\[\mathbf{положительным\ \ числом}\mathbf{.}\]

\[\boxed{\mathbf{5.}}\]

\[Отложим\ от\ начала\ координат\ \]

\[\text{O\ }единичные\ векторы\ \overrightarrow{i}\ и\ \overrightarrow{j}\ так,\]

\[чтобы\ их\ направления\ \]

\[совпадали\ с\ направлениями\ \]

\[осей\ Ox\ и\ \text{Oy}\ соответственно.\]

\[Векторы\ \overrightarrow{i}\ и\ \overrightarrow{j}\ называют\ \]

\[координатными\ векторами.\]

\[\boxed{\mathbf{6.}}\]

\[Утверждение:\]

\[любой\ вектор\ можно\ \]

\[разложить\ по\ координатным\ \]

\[векторам,\ причем\]

\[коэффициенты\ разложения\ \]

\[определяются\ единственным\ \]

\[образом.\]

\[Доказательство.\]

\[Координатные\ векторы\ \overrightarrow{i}\ и\ \overrightarrow{j}\ \]

\[лежат\ на\ перпендикулярных\ \]

\[прямых\]

\[поэтому\ координатные\ \]

\[векторы\ не\ коллинеарны.\]

\[Значит,\ по\ теореме\ \]

\[о\ разложении\ вектора\ по\ двум\ \]

\[не\ коллинеарным\ векторам,\]

\[\ любой\ вектор\ \overrightarrow{p}\ можно\ \]

\[разложить\ по\ координатным\ \]

\[векторам,\ то\ есть\ представить\ \]

\[в\ виде:\]

\[\overrightarrow{p} = x\overrightarrow{i} + y\overrightarrow{j}.\]

\[Причем\ коэффициенты\ \]

\[разложения\ x\ и\ \text{y\ }\]

\[определяются\ единственным\]

\[образом.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{7.}}\]

\[Если\ вектор\ \overrightarrow{p}\ разложить\ \]

\[по\ координатным\ векторам:\]

\[\overrightarrow{p} = x\overrightarrow{i} + y\overrightarrow{j},\ то\ коэффициенты\ \]

\[разложения\ \text{x\ }и\ \text{y\ }называются\]

\[координатами\ вектора\ \overrightarrow{p}\ \]

\[в\ данной\ системе\ координат.\]

\[Записывают\ так:\]

\[\overrightarrow{p}\left\{ x;y \right\}.\]

\[Координатные\ вектора:\]

\[\overrightarrow{i}\left\{ 1;0 \right\};\]

\[\overrightarrow{j}\left\{ 0;1 \right\}.\]

\[Координаты\ равных\ векторов\ \]

\[соответственно\ равны.\]

\[\boxed{\mathbf{8.}}\]

\[Каждая\ координата\ суммы\ \]

\[двух\ и\ более\ векторов\ равна\ \]

\[сумме\ соответствующих\ \]

\[координат\ этих\ векторов.\]

\[Дано:\]

\[\overrightarrow{a}\left\{ x_{1};y_{1} \right\};\]

\[\overrightarrow{b}\left\{ x_{2};y_{2} \right\};\]

\[\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}.\]

\[Доказать:\]

\[\overrightarrow{c}\left\{ x_{1} + x_{2};y_{1} + y_{2} \right\}\text{.\ }\]

\[Доказательство.\]

\[\overrightarrow{a} = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j};\]

\[\overrightarrow{b} = x_{2}\overrightarrow{i} + y_{2}\overrightarrow{j}.\]

\[Складываем\ равенства\ \]

\[и\ применяем\ свойства\ \]

\[сложения\ векторов\]

\[и\ умножения\ вектора\ \]

\[на\ число:\]

\[\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} =\]

\[= x_{1}\overrightarrow{i} + x_{2}\overrightarrow{i} + y_{1}\overrightarrow{j} + y_{2}\overrightarrow{j} =\]

\[= \left( x_{1} + x_{2} \right)\overrightarrow{i} + \left( y_{1} + y_{2} \right)\overrightarrow{j}.\]

\[Следовательно,\ \overrightarrow{c}\ имеет\ \]

\[координаты:\]

\[\overrightarrow{c}\left\{ x_{1} + x_{2};\ y_{1} + y_{2} \right\}.\]

\[Что\ и\ требовалось\ доказать.\]

\[Каждая\ координата\ разности\ \]

\[двух\ векторов\ равна\ разности\]

\[соответствующих\ координат\ \]

\[этих\ векторов.\]

\[Дано:\]

\[\overrightarrow{a}\left\{ x_{1};y_{1} \right\};\]

\[\overrightarrow{b}\left\{ x_{2};y_{2} \right\};\]

\[\overrightarrow{c} = \overrightarrow{a} - \overrightarrow{b}.\]

\[Доказать:\]

\[\overrightarrow{c}\left\{ x_{1} - x_{2};y_{1} - y_{2} \right\}\text{.\ }\]

\[Доказательство.\]

\[\overrightarrow{a} = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j};\]

\[\overrightarrow{b} = x_{2}\overrightarrow{i} + y_{2}\overrightarrow{j}.\]

\[Вычитаем\ равенства\ \]

\[и\ применяем\ свойства\ \]

\[сложения\ векторов\]

\[и\ умножения\ вектора\ \]

\[на\ число:\]

\[\overrightarrow{c} = \overrightarrow{a} - \overrightarrow{b} =\]

\[= x_{1}\overrightarrow{i} - x_{2}\overrightarrow{i} + y_{1}\overrightarrow{j} - y_{2}\overrightarrow{j} =\]

\[= \left( x_{1} - x_{2} \right)\overrightarrow{i} + \left( y_{1} - y_{2} \right)\overrightarrow{j}.\]

\[Следовательно,\ \overrightarrow{c}\ имеет\ \]

\[координаты:\]

\[\overrightarrow{c}\left\{ x_{1} - x_{2};\ y_{1} - y_{2} \right\}.\]

\[Что\ и\ требовалось\ доказать.\]

\[Каждая\ координата\ \]

\[произведения\ вектора\ \]

\[на\ число\ равна\ произведению\ \]

\[соответствующей\ координаты\ \]

\[вектора\ на\ это\ число.\]

\[Дано:\]

\[\overrightarrow{a}\left\{ x;y \right\};\]

\[k - число;\]

\[\overrightarrow{c} = k\overrightarrow{a}.\]

\[Доказать:\]

\[\overrightarrow{c}\left\{ kx;ky \right\}\text{.\ }\]

\[Доказательство.\]

\[\overrightarrow{a} = x\overrightarrow{i} + y\overrightarrow{j}.\]

\[Умножим\ равенство\ на\ число\ \]

\[\text{k\ }и,\ используя\ свойства\ \]

\[умножения\ вектора\ на\ число,\ \]

\[получим:\]

\[\overrightarrow{c} = k\overrightarrow{a} = kx\overrightarrow{i} + ky\overrightarrow{j}.\]

\[Координаты\ вектора:\]

\[\overrightarrow{c}\left\{ kx;ky \right\}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{9.}}\]

\[Вектор,\ который\ соединяет\ \]

\[начало\ координат\ с\ данной\ \]

\[точкой,называется\ радиус -\]

\[вектором.\]

\[Координаты\ точки\ \text{M\ }равны\ \]

\[соответствующим\ \]

\[координатам\ ее\ радиус -\]

\[вектора.\]

\[Дано:\]

\[M(x;y);\]

\[\overrightarrow{\text{OM}} = \overrightarrow{OM_{1}} + \overrightarrow{OM_{2}} - радиус -\]

\[вектор.\]

\[Доказать:\]

\[\overrightarrow{OM_{1}} = x\overrightarrow{i};\]

\[\overrightarrow{OM_{2}} = y\overrightarrow{j}.\]

\[Доказательство.\]

\[1)\ x > 0:\]

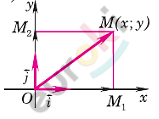
\[x = OM_{1};\]

\[векторы\ \overrightarrow{OM_{1}}\ и\ \overrightarrow{i}\ сонаправлены.\]

\[Тогда:\]

\[\overrightarrow{OM_{1}} = OM_{1} \cdot \overrightarrow{i} = x\overrightarrow{i}.\]

\[2)\ x < 0:\]

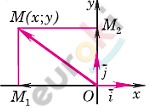
\[x = - OM_{1};\]

\[векторы\ \overrightarrow{OM_{1}}\ и\ \overrightarrow{i}\ \]

\[противоположно\ направлены.\]

\[Тогда:\]

\[\overrightarrow{OM_{1}} = - OM_{1} \cdot \overrightarrow{i} = x\overrightarrow{i}.\]

\[3)\ x = 0:\]

\[\overrightarrow{OM_{1}} = 0;\ \ \]

\[равенство\ \overrightarrow{OM_{1}} = x\overrightarrow{i} - будет\ \]

\[справедливо.\]

\[Получаем,\ что\ в\ любом\ случае\]

\[\ \overrightarrow{OM_{1}} = x\overrightarrow{i}.\]

\[Аналогично\ доказывается,\ что\ \]

\[\overrightarrow{OM_{2}} = y\overrightarrow{j}.\]

\[Следовательно:\]

\[\overrightarrow{\text{OM}} = \overrightarrow{OM_{1}} + \overrightarrow{OM_{2}} = x\overrightarrow{i} + y\overrightarrow{j}.\]

\[Значит:\]

\[координаты\ радиуса\ \overrightarrow{\text{OM}}\ \]

\[равны\ \left\{ x;y \right\};то\ есть\ равны\ \]

\[соответствующим\ точками\ \text{M.}\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{10.}}\]

\[Рассмотрим\ вектор\ \overrightarrow{\text{AB}}\ \]

\[в\ прямоугольной\ системе\ \]

\[координат\ Oxy\ и\ выразим\ его\ \]

\[координаты\ через\ \]

\[координаты\ его\ начала\ \text{A\ }\]

\[и\ конца\ B.\]

\[Пусть\ A\left( x_{1};y_{1} \right);\ \ B\left( x_{2};y_{2} \right).\]

\[Вектор\ \overrightarrow{\text{AB}}\ равен\ разности\ \]

\[векторов\ \overrightarrow{\text{OB}}\ и\ \overrightarrow{\text{OA}}:\]

\[его\ координаты\ равны\ \]

\[разностям\ соответствующих\ \]

\[векторов\ \overrightarrow{\text{OB}}\ и\ \overrightarrow{\text{OA}}.\]

\[\overrightarrow{\text{OB}}\ и\ \overrightarrow{\text{OA}} - радиус - векторы\ \]

\[точек\ A\ и\ B:\]

\[\overrightarrow{\text{OB}}\left\{ x_{2};y_{2} \right\};\ \ \ \overrightarrow{\text{OA}}\left\{ x_{1};y_{1} \right\}.\]

\[Следовательно,\ вектор\ \overrightarrow{\text{AB}}\ \]

\[имеет\ координаты:\]

\[\left\{ x_{2} - x_{1};\ y_{2} - y_{1} \right\}.\]

\[Вывод:\]

\[каждая\ координата\ вектора\ \]

\[равна\ разности\ \]

\[соответствующих\ координат\ \]

\[его\ начала\ и\ конца.\]

\[\boxed{\mathbf{11.}}\]

\[Каждая\ координата\ середины\ \]

\[отрезка\ равна\ полусумме\ \]

\[соответствующих\ координат\ \]

\[его\ концов.\]

\[Дано:\]

\[система\ координат\ Oxy;\]

\[A\left( x_{1};y_{1} \right);\]

\[B\left( x_{2};y_{2} \right);\]

\[\text{C\ }середина\ \text{AB.}\]

\[Решение.\]

\[C - середина\ AB:\]

\[\overrightarrow{\text{OC}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OB}} \right).\ \ \ \ \ \ (1)\]

\[Координаты\ векторов\ \]

\[\overrightarrow{\text{OC}},\ \overrightarrow{\text{OA}},\ \overrightarrow{\text{OB}}\ равны\ \]

\[соответствующим\ \]

\[координатам\ точек\ C;A;B:\]

\[\overrightarrow{\text{OC}}\left\{ x;y \right\};\ \ \overrightarrow{\text{OA}}\left\{ x_{1};y_{1} \right\};\ \]

\[\overrightarrow{\text{OB}}\left\{ x_{2};y_{2} \right\}.\]

\[Запишем\ равенство\ (1)\ \]

\[в\ координатах:\]

\[\left\{ x;y \right\} = \left\{ \frac{x_{1} + x_{2}}{2};\frac{y_{1} + y_{2}}{2} \right\}.\]

\[Следовательно:\]

\[x = \frac{x_{1} + x_{2}}{2};\ \ \ \ y = \frac{y_{1} + y_{2}}{2}.\]

\[\boxed{\mathbf{12.}}\]

\[Докажем,\ что\ длина\ вектора\ \]

\[\overrightarrow{a}\left\{ x;y \right\}\ вычисляется\ \]

\[по\ формуле:\]

\[\left| \overrightarrow{a} \right| = \sqrt{x^{2} + y^{2}}.\]

\[Отложим\ от\ начала\ координат\ \]

\[вектор\ \overrightarrow{\text{OA}} = \overrightarrow{a}\ и\ проведем\ \]

\[через\ точку\ \text{A\ }перпендикуляры\ \]

\[AA_{2}\ и\ AA_{2}\ к\ осям\ \text{Ox\ }и\ \text{Oy.}\]

\[Координаты\ точки\ A\ равны\ \]

\[координатам\ вектора\ \]

\[\overrightarrow{\text{OA}}:\ \ (x;y).\]

\[Тогда:\]

\[OA_{1} = |x|;\ \ \ \]

\[AA_{1} = OA_{2} = |y|;\]

\[x \neq 0;\ \ y \neq 0.\]

\[По\ теореме\ Пифагора:\]

\[OA = \sqrt{OA_{1}^{2} + AA_{1}^{2}} = \sqrt{x^{2} + y^{2}}.\]

\[Так\ как\ \left| \overrightarrow{a} \right| = \left| \overrightarrow{\text{OA}} \right| = OA:\]

\[\left| \overrightarrow{a} \right| = \sqrt{x^{2} + y^{2}}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{13.}}\]

\[Расстояние\ между\ двумя\ \]

\[точками.\]

\[Пусть\ точка\ M_{1}\left( x_{1};y_{1} \right);\]

\[точка\ M_{2}\left( x_{2};y_{2} \right).\]

\[Выразим\ расстояние\ \text{d\ }между\ \]

\[точками\ M_{1}\ и\ M_{2}\ через\ \]

\[их\ координаты.\]

\[Рассмотрим\ вектор\ \ \overrightarrow{M_{1}M_{2}}.\ Его\ \]

\[координаты\ равны\ \]

\[\left\{ x_{2} - x_{1};y_{2} - y_{1} \right\}.\]

\[Следовательно,\ длина\ этого\ \]

\[вектора\ может\ быть\ найдена\ \]

\[по\ формуле:\]

\[\left| \overrightarrow{M_{1}M_{2}} \right| =\]

\[= \sqrt{\left( x_{2} - x_{1} \right)^{2} + \left( y_{2} - y_{1} \right)^{2}}.\]

\[Но\ \left| \overrightarrow{M_{1}M_{2}} \right| = d.\]

\[Таким\ образом,\ расстояние\]

\[\ \text{d\ }между\ точками\ M_{1}(x;y)\ и\ \]

\[M_{2}\left( x_{2};y_{2} \right)\ выражаются\ \]

\[формулой:\]

\[d = \sqrt{\left( x_{2} - x_{1} \right)^{2} + \left( y_{2} - y_{1} \right)^{2}}.\]

\[\boxed{\mathbf{14.}}\]

\[\mathbf{Дано:}\]

\[точки\ \text{A\ }и\ B;\]

\[k - данное\ число;\]

\[AM^{2} + BM^{2} = k^{2}.\]

\[\mathbf{Найти:}\]

\[множество\ точек\ \text{M.}\]

\[\mathbf{Решение.}\]

\[1)\ Введем\ систему\ координат:\]

\[A(0;0);B(a;0);M(x;y);\]

\[\left\{ \begin{matrix} AM^{2} = x^{2} + y^{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ } \\ BM^{2} = (a - x)^{2} + y^{2} \\ \end{matrix}. \right.\ \]

\[2)\ x^{2} + y^{2} + (a - x)^{2} + y^{2} = k^{2}\]

\[2x^{2} + 2y^{2} - 2ax = k^{2} - a^{2}\]

\[2\left( x^{2} - ax + \frac{a^{2}}{4} - \frac{a^{2}}{4} \right) + 2y^{2} =\]

\[= k^{2} - a^{2}\]

\[2\left( x - \frac{a}{2} \right)^{2} + 2y^{2} =\]

\[= k^{2} - a^{2} + \frac{a^{2}}{2} = k^{2} - \frac{a^{2}}{2}\]

\[\left( x - \frac{a}{2} \right)^{2} + y^{2} = \frac{2k^{2} - a^{2}}{4}\]

\[3)\ Множество\ всех\ точек\ M:\]

\[окружность\ с\ центром\ в\ точке\]

\[\ \left( \frac{a}{2};0 \right)\ и\ R = \sqrt{\frac{2k^{2} - a^{2}}{4}};\]

\[но\ 2k^{2} - a^{2} \geq 0 \Longrightarrow 2k^{2} \geq a^{2}.\]

\[\boxed{\mathbf{15.}}\]

\[Уравнением\ линии\ L\ заданной\ \]

\[плоскости\ системы\ координат\ \]

\[\text{Oxy\ }называют\ уравнение\ \]

\[с\ двуми\ переменными\ x\ и\ y,\ \]

\[имеющее\ следующие\ \]

\[свойства:\]

\[1)\ если\ точка\ принадлежит\ \]

\[линии\ L,\ то\ ее\ координаты\ \]

\[являются\ решением\ данного\ \]

\[уравнения;\]

\[2)\ любое\ решение\ (x;y)\ \]

\[данного\ уравнения\ является\ \]

\[координатами\ точки,\ \]

\[принадлежащей\ линии\ L.\]

\[Пример\ уравнения:\]

\[y = x - 4.\]

\[\boxed{\mathbf{16.}}\]

\[Выведем\ уравнение\ \]

\[окружности\ радиуса\ r\ \]

\[с\ центром\ C\ в\ заданной\ \]

\[прямоугольной\ системе\ \]

\[координат.\ \]

\[Пусть\ точка\ C\ \ имеет\ \]

\[координаты\ \left( x_{0};y_{0} \right).\]

\[Расстояние\ \ от\ \ произвольной\ \ \]

\[точки\ M\ (x;y)\ до\ \ точки\ \ C\ \ \]

\[вычисляется\ \ по\ формуле:\]

\[Если\ \ точка\ \ M\ \ лежит\ на\ \ \]

\[данной\ \ окружности,\ то\ \ \]

\[MC = r;\]

\[MC^{2} = r^{2}.\]

\[То\ есть\ координаты\ точки\ M\ \]

\[удовлетворяют\ уравнению:\]

\[\left( x - x_{0} \right)^{2} + \left( y - y_{0} \right)^{2} = r^{2}.\]

\[Если\ точка\ M(x;y)\ не\ лежит\ \]

\[на\ данной\ окружности:\]

\[MC^{2} \neq r^{2}\text{.\ }\]

\[Значит,\ координаты\ точки\ M\ \]

\[не\ удовлетворяют\ \]

\[уравнению\ (1).\]

\[Следовательно,\ \]

\[в\ прямоугольной\ системе\ \]

\[координат\ уравнение\]

\[окружности\ радиуса\ \text{r\ }\]

\[с\ центром\ в\ точке\ C\left( x_{0};y_{0} \right):\]

\[\left( x - x_{0} \right)^{2} + \left( y - y_{0} \right)^{2} = r^{2}.\]

\[\boxed{\mathbf{17.}}\]

\[Частный\ случай\ уравнения\ \]

\[окружности\ радиуса\ \text{r\ }\]

\[с\ центром\ в\ начале\ координат:\]

\[x^{2} + y^{2} = r^{2}.\]

\[\boxed{\mathbf{18.}}\]

\[Выведем\ \ уравнение\ \ данной\ \ \]

\[прямой\ \ l\ \ в\ \ заданной\ \ \]

\[прямоугольной\ системе\ \]

\[координат.\ \ Отметим\ \ две\ \ \]

\[точки\ A\left( x_{1};y_{1} \right);B\left( x_{2};y_{2} \right)\ так,\]

\[чтобы\ прямая\ \ l\ \ была\ \ \]

\[серединным\ \ \]

\[перпендикуляром\ \ к\ отрезку\ \]

\[\text{AB.}\]

\[Если\ точка\ M(x;y)\ лежит\ на\ \]

\[прямой\ l,\ то\ AM = BM;\]

\[AM^{2} = BM^{2}.\]

\[Координаты\ точки\ M\ \]

\[удовлетворяют\ уравнению:\]

\[\left( x - x_{1} \right)^{2} + \left( y - y_{1} \right)^{2} =\]

\[= \left( x - x_{2} \right)^{2} + \left( y - y_{2} \right)^{2}.\ \ \ \ (1)\]

\[Если\ точка\ \text{M\ }не\ лежит\ на\ \]

\[прямой\ l,\ то\ AM^{2} \neq BM^{2}\ \]

\[и\ координаты\ точки\ M\ не\ \]

\[удовлетворяют\ уравнению\ (1).\]

\[Следовательно,\ уравнение\ (1)\ \]

\[является\ \ уравнением\ \ прямой\ \ \]

\[l\ \ в\ заданной\ \ системе\ \ \]

\[координат.\ \ После\ \ возведения\ \]

\[выражений\ в\ скобках\ \ \]

\[в\ \ квадрат\ \ и\ \ приведения\ \]

\[подобных\ \ членов\ \ \]

\[уравнение\ \ (1)\ принимает\ \ \]

\[вид:\]

\[ax + by + c = 0;\]

\[где\ a = 2 \cdot \left( x_{1} - x_{2} \right);\ \ \]

\[b = 2 \cdot \left( y_{1} - y_{2} \right);\ \ \]

\[c = x_{2}^{2} + y_{2}^{2} - x_{1}^{2} - y_{1}^{2}.\]

\[Так\ как\ A\ и\ B - различные\ \]

\[точки,\ то\ хотя\ бы\ одна\ \]

\[из\ разностей\ \left( x_{1} - x_{2} \right)\ и\]

\[\ \left( y_{1} - y_{2} \right)\ не\ равна\ нулю.\]

\[То\ есть,\ хотя\ бы\ один\ из\ \]

\[коэффициентов\ a\ и\ b\ отличен\ \]

\[от\ нуля.\ \]

\[Таким\ образом,\ уравнение\ \]

\[прямой\ \ в\ \ прямоугольной\ \ \]

\[системе\ \ координат\ \ является\ \]

\[\ уравнением\ \ первой\ \ степени.\]

\[\boxed{\mathbf{19.}}\]

\[Уравнение\ прямой\ \]

\[ax + by + c = 0,\ если\ \text{b\ }\]

\[отлично\ от\ нуля:\]

\[y = kx + d.\]

\[k = - \frac{a}{b};\ \ d = - \frac{c}{b}.\]

\[k - угловой\ коэффициент\ \]

\[прямой,\ заданной\ этим\ \]

\[уравнением.\]

\[\boxed{\mathbf{20.}}\]

\[Две\ параллельные\ прямые,\ \]

\[не\ параллельные\ оси\ \text{Oy},\ \]

\[имеют\ одинаковые\ угловые\ \]

\[коэффициенты.\]

\[Дано:\]

\[l_{1} \parallel l_{2};\]

\[M_{1};\ C_{1} \in l_{1};\]

\[M_{2};C_{2} \in l_{2}.\]

\[Доказать:\]

\[k_{1} = k_{2}.\]

\[Доказательство.\]

\[Пусть\ точки\ M_{1}\left( x_{1}y_{1} \right)и\ \]

\[M_{2}\left( x_{2};y_{1} \right)имеют\ равные\ \]

\[ординаты:\]

\[M_{1}M_{2} \parallel Ox.\]

\[Точки\ C_{1}(x_{3};0);C_{2}(x_{4};0) \in Ox.\ \]

\[C_{1}M_{1}M_{2}C_{2} - параллелограмм:\]

\[l_{1} \parallel l_{2} - по\ условию;\]

\[M_{1}M_{2} \parallel Ox - по\ построению.\]

\[По\ свойству\ параллелограмма:\]

\[M_{1}M_{2} = C_{1}C_{2};\]

\[C_{1}M_{1} = C_{2}M_{2}.\]

\[Отсюда:\]

\[C_{1}M_{1} = \sqrt{\left( x_{1} - x_{3} \right)^{2} + \left( y_{1} - 0 \right)^{2}};\]

\[C_{2}M_{2} = \sqrt{\left( x_{2} - x_{4} \right)^{2} + \left( y_{1} - 0 \right)^{2}}.\]

\[Получаем:\]

\[\sqrt{\left( x_{1} - x_{3} \right)^{2} + \left( y_{1} - 0 \right)^{2}} =\]

\[= \sqrt{\left( x_{2} - x_{4} \right)^{2} + \left( y_{1} - 0 \right)^{2}}\]

\[\left( x_{1} - x_{3} \right)^{2} + \left( y_{1} - 0 \right)^{2} =\]

\[= \left( x_{2} - x_{4} \right)^{2} + \left( y_{1} - 0 \right)^{2}\]

\[\left( x_{1} - x_{3} \right)^{2} + y_{1}^{2} =\]

\[= \left( x_{2} - x_{4} \right)^{2} + y_{1}^{2}\]

\[\left( x_{1} - x_{3} \right)^{2} = \left( x_{2} - x_{4} \right)^{2}\]

\[x_{1} - x_{3} = x_{2} - x_{4}.\]

\[Найдем\ коэффициенты:\]

\[k_{1} = - \frac{a_{1}}{b_{1}} = - \frac{2\left( x_{1} - x_{3} \right)}{2y_{1}} =\]

\[= - \frac{2\left( x_{2} - x_{4} \right)}{- 2y_{1}} = - \frac{a_{2}}{b_{2}} = k_{2}.\]

\[Что\ и\ требовалось\ доказать.\]

\[Если\ две\ прямые\ имеют\ \]

\[одинаковые\ угловые\ \]

\[коэффициенты,\ то\ эти\]

\[прямые\ параллельны.\]

\[Дано:\]

\[k_{1} = k_{2};\]

\[M_{1};\ C_{1} \in l_{1};\]

\[M_{2};C_{2} \in l_{2}.\]

\[Доказать:\]

\[l_{1} \parallel l_{2}.\]

\[Доказательство.\]

\[Пусть\ точки\ M_{1}\left( x_{1}y_{1} \right)и\ \]

\[M_{2}\left( x_{2};y_{1} \right)имеют\ равные\ \]

\[ординаты:\]

\[M_{1}M_{2} \parallel Ox.\]

\[Точки\ C_{1}(x_{3};0);C_{2}(x_{4};0) \in Ox.\ \]

\[k_{1} = k_{2}:\]

\[- \frac{2\left( x_{1} - x_{3} \right)}{2y_{1}} = - \frac{2\left( x_{2} - x_{4} \right)}{- 2y_{1}}\]

\[x_{1} - x_{3} = x_{2} - x_{4}\]

\[\left( x_{1} - x_{3} \right)^{2} = \left( x_{2} - x_{4} \right)^{2}\]

\[C_{1}M_{1} =\]

\[= \sqrt{\left( x_{1} - x_{3} \right)^{2} + \left( y_{1} - 0 \right)^{2}} =\]

\[= \sqrt{\left( x_{2} - x_{4} \right)^{2} + \left( y_{1} - 0 \right)^{2}} =\]

\[= C_{2}M_{2}.\]

\[Опустим\ высоты\ M_{1}N_{1}\ и\ M_{2}H_{2}.\]

\[⊿C_{1}M_{1}H_{1} = ⊿C_{2}M_{2}H_{2} -\]

\[по\ гипотенузе\ и\ катету:\]

\[M_{1}H_{1} = M_{2}H_{2} - расстояние\ \]

\[между\ параллельными\ \]

\[прямыми;\]

\[C_{1}M_{1} = C_{2}M_{2} - смотри\ выше.\]

\[В\ равных\ треугольниках\ \]

\[напротив\ соответственно\ \]

\[равных\ сторон\ лежат\ равные\ \]

\[углы:\]

\[\angle M_{1}C_{1}H_{1} = \angle M_{2}C_{2}H_{2}.\]

\[Если\ при\ пересечении\ двух\ \]

\[прямых\ секущей\ \]

\[соответственные\ углы\ равны,\]

\[\ то\ прямые\ параллельны:\]

\[l_{1} \parallel l_{2}.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\mathbf{21.}}\]

\[M_{0}\left( x_{0};y_{0} \right);\ \ \]

\[l \parallel Ox:\]

\[y = y_{0}.\]

\[l \parallel Oy:\]

\[x = x_{0}.\]

\[\boxed{\mathbf{22.}}\]

\[Ось\ O\text{x\ }имеет\ уравнение\ y = 0.\]

\[Ось\ Oy\ имеет\ уравнение\ x = 0.\]

\[\boxed{\mathbf{23.}}\]

\[Окружности\ \ с\ \ общим\ \ \]

\[центром\ \ и\ \ различными\ \ \]

\[радиусами\ \ называются\ \ \]

\[концентрическими.\ \ В\ \ этом\ \ \]

\[случае\ \ окружности\ \ не\ \ имеют\ \]

\[общих\ точек,\ все\ \ точки\ \ одной\ \ \]

\[из\ \ окружностей\ являются\ \ \]

\[внутренними\ \ точками\ \ \]

\[относительно\ другой.\]

\[Если\ центры\ O_{1}\ и\ O_{2}\ двух\ \]

\[окружностей\ с\ радиусом\ \text{R\ }и\ \]

\[\text{r\ }не\ совпадают;\]

\[O_{1}O_{2} = d:\]

\[1)\ при\ R - r < d < R + r;\ \ \]

\[R \geq r - окружности\ \]

\[пересекаются;\]

\[2)\ при\ d = R + r -\]

\[окружности\ касаются\ \]

\[внешним\ образом;\]

\[3)\ при\ d = R - r;R > r -\]

\[окружности\ касаются\ \]

\[внутренним\ образом;\]

\[4)\ при\ d > R + r - окружности\ \]

\[не\ имеют\ общих\ точек;\]

\[окружность\ с\ центром\ O_{2}\ \]

\[расположена\ вне\ окружности\ \]

\[с\ центром\ O_{1};\]

\[5)\ при\ d < R - r;\ \ R > r -\]

\[окружности\ не\ имеют\ общих\ \]

\[точек;\]

\[окружность\ с\ центром\ O_{2}\ \]

\[равсположена\ внутри\ \]

\[окружности\ с\ центром\ O_{1}.\]

\[\boxed{\mathbf{24.}}\]

\[Задачи\ 981\ и\ 984\ в\ учебнике.\]