ГДЗ по геометрии 11 класс. Атанасян ФГОС 863

\[\boxed{\mathbf{863.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

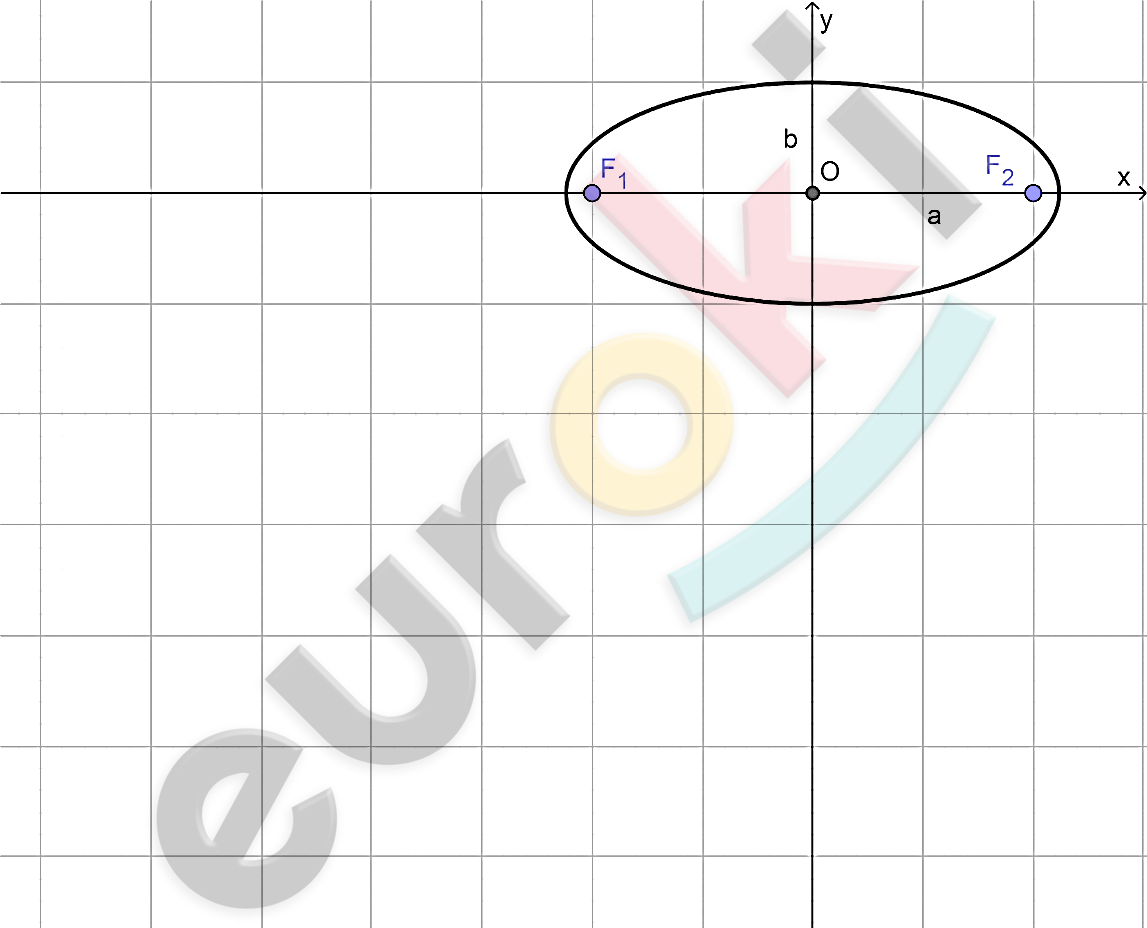
\[Дано:\]

\[F_{1}F_{2} = 4\sqrt{2};\]

\[\frac{a}{b} = 3.\]

\[Найти:\]

\[\textbf{а)}\ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1;\]

\[\textbf{б)}\ e - ?;\]

\[\textbf{в)}\ x = \frac{a^{2}}{c}.\]

\[Решение.\]

\[Так\ как\ расстояние\ между\ \]

\[фокусами\ равно\ F_{1}F_{2} = 4\sqrt{2}:\ \]

\[c = OF_{1} = OF_{2} = 2\sqrt{2}.\]

\[По\ свойству\ эллипса:\]

\[b^{2} = a^{2} - c^{2}\ \]

\[\frac{a^{2}}{a^{2} - c^{2}} = \frac{a^{2}}{b^{2}} = 3^{2} = 9\]

\[a^{2} = 9a^{2} - 9c^{2}\ \]

\[8a^{2} = 9c^{2} = 9 \bullet \left( 2\sqrt{2} \right)^{2} = 72\]

\[a = \sqrt{\frac{72}{8}} = \sqrt{9} = 3.\]

\[b = 9 - \left( 2\sqrt{2} \right)^{2} = 1.\]

\[\textbf{а)}\ Каноническое\ уравнение\ \]

\[эллипса:\ \ \]

\[\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = \frac{x^{2}}{9} + y^{2} = 1.\]

\[\textbf{б)}\ Эксцентриситет\ равен:\ \ \]

\[e = \frac{c}{a} = \frac{2\sqrt{2}}{3}.\]

\[\textbf{в)}\ Запишем\ уравнения\ \]

\[директрис:\]

\[x = \frac{a^{2}}{c} = \frac{9}{2\sqrt{2}} = \frac{9\sqrt{2}}{4};\text{\ \ }\]

\[x = - \frac{9\sqrt{2}}{4}.\]

\[\mathbf{Ответ}\mathbf{:\ \ }\mathbf{а)\ }\frac{x^{2}}{9} + y^{2} = 1;\ \ \]

\[\textbf{б)}\ e = \frac{2\sqrt{2}}{3}\text{\ \ };\ \ \]

\[\textbf{в)}\ x = - \frac{9\sqrt{2}}{4};\ \ \ x = \frac{9\sqrt{2}}{4}.\]