Решебник по геометрии 11 класс. Атанасян ФГОС 834

\[\boxed{\mathbf{834.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

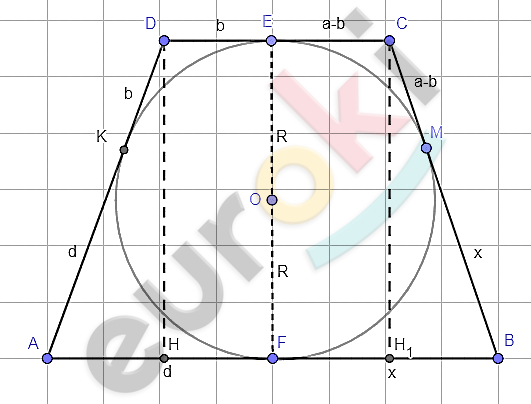
\[ABCD - трапеция;\]

\[AB \parallel DC;\]

\[AB > DC;\]

\[DC = a;\ \]

\[DK = b;\]

\[AK = d.\]

\[Найти:\]

\[S_{\text{ABCD}}.\]

\[Решение.\]

\[1)\ \ Отметим\ точки\ касания\ \]

\[окружности\ и\ сторон\ \]

\[трапеции:\]

\[E \in DC;\ \ M \in CB;\ \ F \in AB.\]

\[Как\ касательные\ из\ одной\ \]

\[точки:\]

\[DE = DK = b;\]

\[CM = CE;\]

\[BM = BF;\]

\[AK = AF = d.\ \]

\[Отсюда:\ \ \]

\[CM = EC = DC - DE = a - b;\]

\[2)\ Опустим\ высоту\ DH:\ \ \]

\[DH = 2R.\]

\[DH^{2} = AD^{2} - AH^{2} =\]

\[= (d + b)^{2} - (d - b)^{2}\]

\[4R^{2} =\]

\[= d^{2} + 2db + b^{2} - d^{2} + 2db - b^{2} =\]

\[= 4db\]

\[R = \sqrt{\text{db}}.\]

\[3)\ Опустим\ высоту\ CH_{1}:\]

\[CH_{1} = DH = 2R.\]

\[Пусть\ BM = BF = x:\]

\[\left( CH_{1} \right)^{2} = BC^{2} - \left( BH_{1} \right)^{2} =\]

\[= (x + a - b)^{2} - (x - a + b)^{2}\]

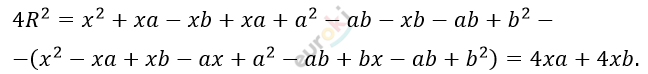
\[4)\ \ 4R^{2} = 4db = 4xa + 4xb\ \]

\[x = \frac{\text{bd}}{a - b}.\]

\[5)\ S_{\text{ABCD}} = \frac{1}{2}DH \bullet (DC + AB) =\]

\[= \frac{1}{2} \bullet 2R \bullet (d + x + a) =\]

\[= \left( d + \frac{\text{bd}}{a - b} + a \right)\sqrt{\text{bd}} =\]

\[= \frac{(d + a)(a - b) + bd}{a - b}\sqrt{\text{bd}} =\]

\[= \frac{da - db + a^{2} - ab + bd}{a - b}\sqrt{\text{bd}} =\]

\[= \frac{a^{2} + a(d - b)}{a - b}\sqrt{\text{bd}}.\]

\[\mathbf{Ответ}\mathbf{:\ }\frac{a^{2} + a(d - b)}{a - b}\sqrt{\text{bd}}.\]