Решебник по геометрии 11 класс. Атанасян ФГОС 816

\[\boxed{\mathbf{816.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[окружность\ O;\]

\[OA - радиус;\]

\[BC\bot OA;\]

\[BE - касательная;\]

\[OA \cap BE = E.\]

\[Доказать:\]

\[BA - биссектриса\ \angle\text{CBE.}\]

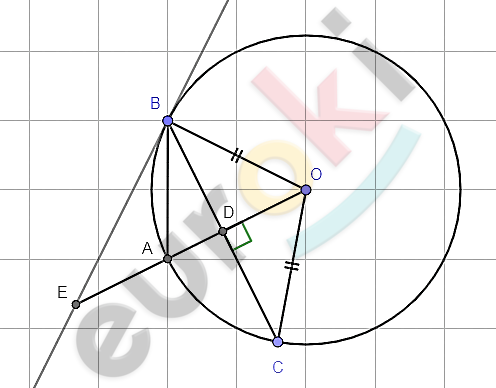
\[Доказательство.\]

\[1)\ Угол\ между\ касательной\ и\ \]

\[хордой\ BA:\]

\[\angle ABE = \frac{1}{2} \cup BA = \frac{1}{2}\angle AOB.\]

\[2)\ Угол\ между\ хордой\ \text{BC\ }и\ \]

\[лучом\ BA:\]

\[\angle ABC = \frac{1}{2} \cup AC = \frac{1}{2}\angle AOC =\]

\[= \frac{1}{2}\angle BOA\ (так\ как\ \mathrm{\Delta}\text{BOC}\]

\[равнобедренный,\ значит\ OD -\]

\[высота\ и\ биссектриса).\]

\[3)\ Таким\ образом:\ \]

\[\angle ABE = \angle ABC = \frac{1}{2}\angle AOB.\]

\[Значит:\]

\[BA - биссектриса\ \angle\text{CBE.}\]

\[Что\ и\ требовалось\ доказать.\]