Решебник по геометрии 11 класс. Атанасян ФГОС 535

\[\boxed{\mathbf{535.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

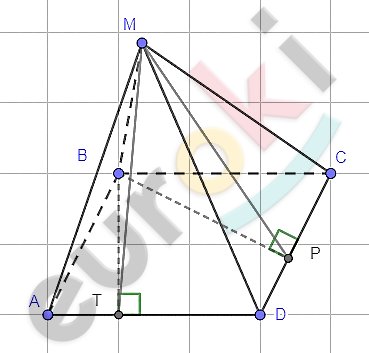
\[MABCD - пирамида;\]

\[MB - высота;\]

\[ABCD - ромб;\]

\[AB = a;\ \ \]

\[\angle MTB = \theta;\]

\[\angle MPB = \theta;\]

\[\angle ABC = \varphi.\]

\[Найти:\]

\[\text{V.}\]

\[Решение.\]

\[1)\ \angle ABC - линейный\ угол\ \]

\[между\ гранями\ MAB\ и\ MCB:\]

\[\angle BAD = \angle BCD = 180{^\circ} - \varphi.\]

\[2)\ Построим\ BT\bot AD\ и\ \]

\[BP\bot CD:\ \]

\[MT\bot AD;\ \ MP\bot CD\ \]

\[3)\ \mathrm{\Delta}BPM = \mathrm{\Delta}BMT:\]

\[\angle MTB = \angle MPB = \theta\ \]

\[(как\ линейные\ углы\ \]

\[двугранных\ углов\ между\ \]

\[боковыми\ гранями\ и\ \]

\[плоскостью\ основания);\]

\[BM - общий\ катет.\]

\[Отсюда:\ \]

\[TB = PB = a \bullet \sin(180{^\circ} - \varphi) =\]

\[= a \bullet \sin\varphi.\]

\[4)\ \mathrm{\Delta}BMT - прямоугольный:\]

\[\frac{\text{MB}}{\text{BT}} = tg\ \theta;\]

\[MB = BT \bullet tg\ \theta;\ \]

\[MB = a \bullet \sin\varphi \bullet tg\ \theta.\]

\[5)\ Площадь\ основания\ \]

\[пирамиды:\]

\[S_{осн} = S_{\text{ABCD}} =\]

\[= AD \bullet AB \bullet \sin{\angle BAD} =\]

\[= a^{2} \bullet \sin{(180{^\circ} - \varphi}) = a^{2} \bullet \sin\varphi.\]

\[6)\ V = \frac{1}{3} \bullet S_{осн} \bullet MB =\]

\[= \frac{1}{3}a^{2} \bullet \sin\varphi \bullet a \bullet \sin\varphi \bullet tg\ \theta =\]

\[= \frac{1}{3} \bullet a^{3} \bullet \sin^{2}\varphi \bullet tg\ \theta.\]

\[\mathbf{Отв}ет:\ \ V = \frac{1}{3} \bullet a^{3} \bullet \sin^{2}\varphi \bullet tg\ \theta.\]