Решебник по геометрии 11 класс. Атанасян ФГОС 385

\[\boxed{\mathbf{385.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[сфера;\]

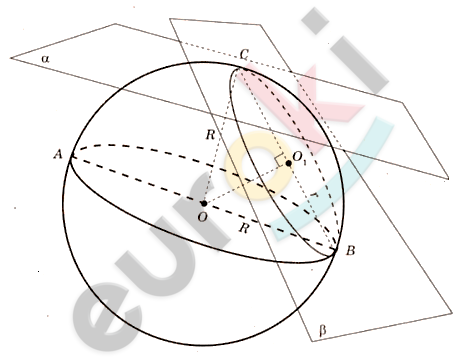
\[R - радиус;\]

\[C - точка\ касания\ плоскости\ \alpha\ \]

\[со\ сферой.\]

\[Найти:\]

\[S_{сеч}.\]

\[Решение.\]

\[OO_{1}\bot BC.\]

\[⊿OO_{1}C = ⊿OO_{1}\text{B\ }\]

\[(прямоугольные):\]

\[OO_{1} - общий\ катет;\]

\[OC = OB = R.\]

\[Отсюда:\]

\[CO_{1} = O_{1}\text{B.}\]

\[O_{1} - центр\ окружности;\]

\[\varphi - угол\ между\ плоскостями\ \]

\[\alpha\ и\ \beta.\]

\[\angle OCB = 90{^\circ} - \varphi:\]

\[⊿BOC - равнобедренный.\]

\[В\ треугольнике\ OO_{1}B:\]

\[O_{1}B = r = R \cdot \cos(90{^\circ} - \varphi) =\]

\[= R \cdot \sin\varphi.\]

\[S_{сеч} = \pi R^{2} = \pi\left( R \cdot \sin\varphi \right)^{2} =\]

\[= \pi R^{2}\text{si}n^{2}\text{φ.}\]

\[Ответ:\ \pi R^{2}\text{si}n^{2}\text{φ.}\]