Решебник по геометрии 11 класс. Атанасян ФГОС 300

\[\boxed{\mathbf{300.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

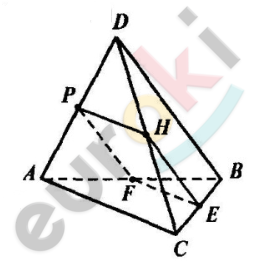
\[AC = a;\]

\[BD = b.\]

\[Найти:\]

\[S_{сеч}.\]

\[Решение.\]

\[AC \parallel плоскости\ сечения:\]

\[линия\ пересечения\ плоскостей\ \]

\[\text{ACD\ }и\ PFE \parallel AC.\]

\[Проведем\ PH \parallel AC.\]

\[Получаем:\]

\[H - середина\ DC;\]

\[PFEH - искомое\ сечение.\]

\[PF \parallel BD;\ \ HE \parallel DB;\ \ \]

\[PF = HE = \frac{1}{2}DB:\]

\[PFEH - параллелограмм.\]

\[PF \parallel DB;\ \ PH \parallel AC;\ \ AC\bot BD:\]

\[PF\bot PH\ (см.\ №261).\]

\[Отсюда:\]

\[PFEH - прямоугольник.\]

\[PH = \frac{1}{2}AC = \frac{1}{2}a;\ \ PF = \frac{1}{2}BD =\]

\[= \frac{1}{2}b:\]

\[S_{сеч} = \frac{1}{2}a \cdot \frac{1}{2}b = \frac{\text{ab}}{4}.\]

\[Ответ:\ \frac{\text{ab}}{4}.\]