Решебник по геометрии 10 класс Атанасян ФГОС Задачи с практическим содержанием.
Задачи с практическим содержанием.
\[\boxed{Задачи\ \ с\ практическим\ содержанием\mathbf{\text{.\ }}\mathbf{ОК\ ГДЗ\ –\ домашка\ на\ }5\mathbf{\ }}\]
1
\[\boxed{\mathbf{1.}}\]
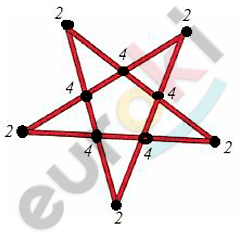
\[Пятиконечная\ звезда - это\ \]
\[граф,\ в\ котором\ 5\ вершин\ \]
\[второй\ степени\ и\ 5\ вершин\ \]
\[четвертой\ степени.\ Все\ степени\ \]
\[четные.Следовательно,\ граф\ \]
\[можно\ нарисовать\ одним\ \]
\[росчерком,\ не\ отрывая\ \]
\[карандаша\ от\ бумаги,\ начиная\ \]
\[с\ любого\ места.Значит,\ можно\ \]
\[изготовить\ звезду\ из\ \]
\[прямолинейной\ рейки,\ начиная\]
\[ее\ изгибать\ с\ любого\ места.\]
2
\[\boxed{\mathbf{2.}}\]

\[Нужно\ доказать,\ что\ N,\ M\ и\ H,\ L\ \]
\[лежат\ в\ одной\ плоскости.\ \]
\[Пусть\ точки\ N\ и\ M\ \]
\[принадлежат\ задней\ грани,\ \]
\[H\ и\ L\ —\ нижней\ грани,\ то\ есть\ \]
\[точка\ пересечения\ NM\ и\ HL\ \]
\[должна\ лежать\ на\ прямой,\ \]
\[принадлежащей\ обеим\ граням,\ \]
\[то\ есть\ AC.\ \]
\[Продлим\ прямые\ NM\ и\ HL\ и\ \]
\[найдем\ точку\ их\ пересечения.\ \]
\[Эта\ точка\ не\ будет\ \]
\[принадлежать\ прямой\ AC.\ \]
\[Значит,\ точки\ N,\ M,\ L,\ H\ не\ \]
\[образуют\ плоский\ \]
\[многоугольник.\ \]
\[Ответ:невозможно.\]
3
\[\boxed{\mathbf{3.}}\]
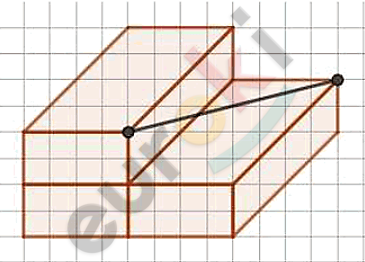
\[\mathbf{Диагональ\ кирпича - это\ }\]
\[\mathbf{отмеченный\ отрезок.}\]
4
\[\boxed{\mathbf{4.}}\]
\[Площадь\ платка\ больше,\ чем\ \]
\[площадь\ всех\ сторон\ куба.\]
\[Значит,\ мы\ точно\ можем\ \]
\[завернуть\ куб\ с\ ребром\ 10\ см\ в\ \]
\[квадратный\ платок\ со\ \]
\[стороной\ 30\ см,\ но\ для\ этого\ \]
\[необходимо\ разместить\ куб\ \]
\[в\ центре\ платка\ и\ развернуть\ \]
\[его\ так,\ чтобы\ диагонали\ \]
\[платка\ проходили\ через\ \]
\[середины\ сторон\ куба.\]
5
\[\boxed{\mathbf{5.}}\]
\[\mathbf{Введём\ наряду\ с\ координатами\ }\]
\[\mathbf{в\ плоскости,\ в\ которой\ }\]
\[\mathbf{движутся\ пешеходы,\ ещё\ и\ }\]
\[\mathbf{третью\ ось\ координат\ –\ ось\ }\]
\[\mathbf{времени.\ }\]
\[\mathbf{Рассмотрим\ графики\ движения\ }\]
\[\mathbf{пешеходов.\ }\]
\[\mathbf{Ясно,\ что\ пешеходы\ }\]
\[\mathbf{встречаются,\ когда\ их\ графики\ }\]
\[\mathbf{движения\ пересекаются.\ }\]
\[\mathbf{Из\ условия\ следует,\ что\ }\]
\[\mathbf{графики\ третьего\ и\ четвёртого\ }\]
\[\mathbf{пешеходов\ лежат\ в\ плоскости,\ }\]
\[\mathbf{заданной\ графиками\ двух\ }\]
\[\mathbf{первых\ пешеходов.\ }\]
\[\mathbf{Поэтому\ графики\ третьего\ и\ }\]
\[\mathbf{четвёртого\ пешеходов\ }\]
\[\mathbf{пересекаются.}\]
6
\[\boxed{\mathbf{6.}}\]
\[При\ плавлении\ объем\ \]
\[конечной\ детали\ равен\ сумме\ \]
\[объемов\ частей:\]
\[V = V_{1} + V_{2} + V_{3} =\]
\[= 3^{3} + 4^{3} + 5^{3} =\]
\[= 27 + 64 + 125 = 216\ см^{3}.\]
\[Найдем\ ребро\ получившегося\ \]
\[куба:\]
\[d^{3} = 216\]
\[d = 6\ см.\]
\[Ответ:6\ см.\]
7
\[\boxed{\mathbf{7.}}\]
\[1)\ V = abc - объем\ кирпича.\]
\[2)\ Плотность:\]
\[\rho = \frac{m}{V} = \frac{m}{\text{abc}} = \frac{3510}{25 \cdot 12 \cdot 6,5} =\]
\[= \frac{3510}{30 \cdot 65} = \frac{117}{65} = \frac{9}{5} =\]
\[= 1,8\ \left( \frac{г}{см^{3}} \right).\]
\[Ответ:1,8\ \frac{г}{см^{3}}.\]
8
\[\boxed{\mathbf{8.}}\]
\[a = 12\ м;b = 6\ м;h = 2\ м;\]
\[l = 10\ м.\]
\[Участок\ является\ прямой\ \]
\[призмой\ с\ трапецией\ в\ \]
\[основании;\ \]
\[ее\ ребро\ перпендикулярно\ \]
\[основанию\ и\ равно\ \text{l.}\]
\[V = S_{осн} \cdot l = \frac{a + b}{2} \cdot hl =\]
\[= \frac{12 + 6}{2} \cdot 2 \cdot 10 = 180\ м^{3}.\]
\[Ответ:180\ м^{3}.\]
9
\[\boxed{\mathbf{9.}}\]
\[a = 20\ м;\ \ \ \ b = 16\ м;h = 2\ м;\]
\[v = 2\ \frac{м}{с};\ t = 1\ мин = 60\ с.\]
\[Столб\ жидкости\ является\ \]
\[прямой\ призмой\ с\ трапецией\ в\ \]
\[основании;\]
\[ее\ ребро\ \bot основанию\ и\ равно\ \]
\[l = vt.\]
\[V = S_{осн} \cdot l = \frac{a + b}{2} \cdot h \cdot vt =\]
\[= \frac{20 + 16}{2} \cdot 2 \cdot 2 \cdot 60 = 4320\ м^{3}.\]
\[Ответ:4320\ м^{3}.\]
10
\[\boxed{\mathbf{10.}}\]
\[\mathbf{Чем\ меньше\ площадь\ сечения\ }\]
\[\mathbf{реки,\ тем\ больше\ скорость\ }\]
\[\mathbf{течения\ реки\ через\ это\ сечение,\ }\]
\[\mathbf{поэтому\ при\ одинаковой\ }\]
\[\mathbf{глубине\ у\ узких\ местах\ русла\ }\]
\[\mathbf{реки\ её\ течение\ быстрее,\ чем\ в\ }\]
\[\mathbf{широких.\ }\]
\[\mathbf{Если\ ширина\ одинаковая,\ а\ }\]
\[\mathbf{глубина\ разная,\ то\ скорость\ }\]
\[\mathbf{течения\ реки\ будет\ быстрее\ }\]
\[\mathbf{там,\ где\ глубина\ меньше.}\]
11
\[\boxed{\mathbf{11.}}\]
\[\mathbf{Для\ отверстий\ в\ виде\ круга\ и\ }\]
\[\mathbf{квадрата\ универсальной\ }\]
\[\mathbf{является\ пробка\ в\ виде\ }\]
\[\mathbf{цилиндра.}\]
\[\mathbf{Усечём\ этот\ цилиндр\ }\]
\[\mathbf{плоскостями,\ проходящими\ }\]
\[\mathbf{через\ диаметр\ верхнего\ }\]
\[\mathbf{основания\ цилиндра\ и\ }\]
\[\mathbf{касающимися\ нижнего\ }\]
\[\mathbf{основания.\ }\]
\[\mathbf{Полученное\ тело\ сохранило\ }\]
\[\mathbf{свойство\ быть\ универсальной\ }\]
\[\mathbf{пробкой\ для\ круга\ и\ квадрата,}\]
\[\mathbf{но\ теперь\ в\ одной\ из\ проекций\ }\]
\[\mathbf{имеет\ вид\ треугольника\ и\ }\]
\[\mathbf{может\ служить\ «пробкой»\ для\ }\]
\[\mathbf{всех\ трёх\ отверстий.}\]

12
\[\boxed{\mathbf{12.}}\]
\[Объем\ воды\ в\ первом\ \]
\[цилиндре:\]
\[V = \pi r_{1}^{2}h_{1} = \frac{\pi}{4}d_{1}^{2}h_{1}.\]
\[Объем\ воды\ во\ втором\ \]
\[цилиндре:\]
\[V = \frac{\pi}{4}d_{2}^{2}h_{2}.\]
\[Получаем\ равенство\ \]
\[(так\ как\ объем\ равный):\]
\[\frac{\pi}{4}d_{1}^{2}h_{1} = \frac{\pi}{4}d_{2}^{2}h_{2}\]
\[\frac{h_{2}}{h_{1}} = \frac{d_{1}^{2}}{d_{2}^{2}} = \frac{15^{2}}{5^{2}}\]
\[\frac{h_{2}}{h_{1}} = \frac{225}{25} = 9\ (раз).\]
\[Ответ:в\ 9\ раз.\]
13
\[\boxed{\mathbf{13.}}\]
\[\mathbf{Объем\ проволоки:}\]
\[V = \pi r^{2}L = \frac{\pi}{4}d^{2}L;\ \ \ V = \frac{m}{\rho}.\]
\[Получаем\ равенство:\]
\[\frac{\pi}{4}d^{2}L = \frac{m}{\rho}\]
\[d = \sqrt{\frac{4m}{\text{πρL}}} = 2\sqrt{\frac{m}{\text{πρL}}} =\]
\[= 2 \cdot \sqrt{\frac{700}{\pi \cdot 8,9 \cdot 10\ 000}} \approx\]
\[\approx 2 \cdot 0,05 \approx 0,1\ см = 1\ мм.\]
\[Ответ:1\ мм.\]
14
\[\boxed{\mathbf{14.}}\]
\[Столб\ воды\ за\ 1\ час:\]
\[V = \frac{\pi}{4}d^{2}l = \frac{\pi}{4}d^{2}vt;\ \ V = qt.\]
\[Пропускная\ способность:\]
\[q = \frac{\pi}{4}d^{2}v;\ \ \ \]
\[d = 10\ см = 0,1\ м;\ \ \ v = 2\ \frac{м}{с} =\]
\[= 7200\ \frac{м}{ч}.\]
\[Подставим:\]
\[q = \frac{\pi}{4} \cdot 0,1^{2} \cdot 7200 \approx 56,5\ \left( \frac{м^{3}}{ч} \right).\]
\[Ответ:56,5\ \frac{м^{3}}{ч}.\]
15
\[\boxed{\mathbf{15.}}\]
\[\mathbf{Нужно\ наклонить\ бочку\ так,\ }\]
\[\mathbf{чтобы\ вода\ подошла\ к\ краю.}\]
\[1)\ Если\ воды\ меньше\ \]
\[половины,\ то\ будет\ видно\ дно\ \]
\[бочки.\]
\[2)\ Если\ воды\ больше\ \]
\[половины,\ дна\ бочки\ видно\ не\ \]
\[будет.\]
16
\[\boxed{\mathbf{16.}}\]
\[L = 2\pi r:\]
\[r = \frac{L}{2\pi} \approx \frac{31,4}{2 \cdot 3,14} = 5\ м.\]
\[h = \sqrt{l^{2} - r^{2}} = \sqrt{{5,4}^{2} - 5^{2}} =\]
\[= \sqrt{0,4 \cdot 10,4} = 0,4\sqrt{26} = \frac{2\sqrt{26}}{5}.\]
\[V = \frac{\pi}{3}r^{2} \cdot \sqrt{l^{2} - r^{2}} =\]
\[= \frac{\pi}{3} \cdot 25 \cdot \frac{2\sqrt{26}}{5} = \frac{10\sqrt{26}}{3}\pi \approx\]
\[\approx 53,4\ м^{3}.\]
\[\rho = \frac{m_{0}}{v_{0}} = \frac{2}{1} = 2\ \left( \frac{т}{м^{3}} \right).\]
\[M = \rho V = 2 \cdot 53,4 = 106,8\ т.\]
\[N = \frac{M}{M_{0}} = \frac{106,8}{3} = 35,6 \approx\]
\[\approx 36\ машин.\]
\[Ответ:36\ машин.\]
17
\[\boxed{\mathbf{17.}}\]
\[Объем\ стога:\]
\[V = V_{цил} + V_{кон} =\]
\[= \pi R^{2}H + \frac{1}{3}\pi R^{2}h =\]
\[= \pi R^{2}\left( H + \frac{h}{3} \right).\]
\[Масса\ стога:\]
\[M = \rho V = \rho\pi R^{2}\left( H + \frac{h}{3} \right) =\]
\[= \pi \cdot 70 \cdot 3^{2}\left( 2 + \frac{2}{3} \right) = 1680\pi \approx\]
\[\approx 5280\ кг.\]
\[Ответ:1680\pi\ или\ 5280\ кг.\]
18
\[\boxed{\mathbf{18.}}\]
\[У\ ведра\ есть\ дно\ и\ боковая\ \]
\[поверхность:\]
\[S = S_{дно} + S_{бок} =\]
\[= \pi r^{2} + \pi(r + R) \cdot l.\]
\[Общая\ поверхность\ при\ \]
\[покраске\ с\ двух\ сторон:\]
\[S_{ведро} = 2\text{S.}\]
\[Площадь\ поверхности\ всех\ \]
\[ведер:\]
\[S_{N} = N \cdot S_{ведро} =\]
\[= 2\text{Nπ}\left( r^{2} + (r + R)l \right) =\]
\[= 2 \cdot 100\pi\left( 0,1^{2} + (0,1 + 0,15) \cdot 0,3 \right) =\]
\[= 2\pi(1 + 7,5) = 17\pi\ \left( м^{2} \right).\]
\[Масса\ краски:\]
\[M = m_{0} \cdot S_{N} = 0,15 \cdot 17\pi \approx 8\ кг.\]
\[Ответ:примерно\ 8\ кг.\]
19
\[\boxed{\mathbf{19.}}\]
\[Объем\ шара\ через\ диаметр:\]
\[V = \frac{4}{3}\pi r^{3} = \frac{4}{3}\pi\left( \frac{d}{2} \right)^{3} = \frac{\pi}{6}d^{3}.\]
\[Отношение\ объемов\ небесных\ \]
\[тел:\]
\[\frac{V_{З}}{V_{Л}} = \frac{\frac{\pi}{6}d_{З}^{3}}{\frac{\pi}{6}d_{Л}^{3}} = \left( \frac{d_{З}}{d_{Л}} \right)^{3} =\]
\[= \left( \frac{12740}{3474} \right)^{3} \approx 49,3\ раза.\]
\[Ответ:примерно\ в\ 49,3\ раза.\]
20
\[\boxed{\mathbf{20.}}\]
\[Объем\ маленьких\ шариков:\]
\[v_{0} = \frac{4}{3}\pi r^{3}.\]
\[Объем\ полученного\ шара:\]
\[V = \frac{4}{3}\pi R^{3};\ \ \ V = nv_{0} = \frac{4}{3}\text{πn}r^{3}.\]
\[Получаем\ равенство:\]
\[\frac{4}{3}\pi R^{3} = \frac{4}{3}\text{πn}r^{3}\]
\[R^{3} = nr^{3}\]
\[R = r^{3}\sqrt{n} = 1 \cdot \sqrt[3]{8} = 1 \cdot 2 =\]
\[= 2\ см.\]
\[Ответ:2\ см.\]
21
\[\boxed{\mathbf{21.}}\]
\[Если\ человек\ находится\ на\ \]
\[южном\ полюсе,\ то\ он\ может\ \]
\[пройти\ 1\ км\ на\ север,\ потом -\]
\[1\ км\ на\ запад;потом - 1\ км\ на\ \]
\[юг.\]
\[Ответ:да,\ если\ начальная\ \]
\[точка - Южный\ полюс.\]
22
\[\boxed{\mathbf{22.}}\]
\[Объем\ цилиндра:\]
\[V = \pi r^{2}h\]
\[h = \frac{V}{\pi r^{2}}.\]
\[Площадь\ поверхности:\]
\[S_{пов} = 2S_{осн} + S_{бок} =\]
\[= 2\pi r^{2} + 2\pi rh =\]
\[= 2\pi r^{2} + 2\pi r \cdot \frac{V}{\pi r^{2}} = 2\pi r^{2} + \frac{2V}{r}.\]
\[Найдем\ производную\ по\ r:\]
\[\left( S_{пов} \right)_{r}^{'} = 4\pi r - \frac{2V}{r^{2}} =\]
\[= \frac{2 \cdot \left( 2\pi r^{3} - V \right)}{r^{2}}.\]
\[Производная\ равна\ 0\ при:\]
\[2\pi r^{3} - V = 0\]
\[r_{0} = \sqrt[3]{\frac{V}{2\pi}}.\]
| \[r\] | \[(0;r_{0})\] | \[r_{0}\] | \[\left( r_{0}; + \infty \right)\] |
|---|---|---|---|
| \[\left( S_{пов} \right)_{r}^{'}\] | \[< 0\] | \[0\] | \[> 0\] |
| \[S_{пов}\] | \[\searrow\] | \[\min\] | \[\nearrow\] |
\[В\ точке\ r_{0} - минимум\ площади\ \]
\[поверхности.\]
\[Найдем\ высоту\ цилиндра:\]
\[h_{0} = \frac{V}{\pi r_{0}^{2}} = \frac{V}{\pi} \cdot \left( \frac{2\pi}{V} \right)^{\frac{2}{3}} = \sqrt[3]{\frac{4V}{\pi}}.\]
23
\[\boxed{\mathbf{23.}}\]
\[\mathbf{Почему\ в\ зеркале\ лево\ и\ право\ }\]
\[\mathbf{меняются,\ а\ верх\ и\ низ\ - \ нет?}\]
\[\mathbf{В\ действительности\ зеркала\ }\]
\[\mathbf{изменяют\ на\ обратную\ }\]
\[\mathbf{последовательность,\ в\ которой\ }\]
\[\mathbf{расположены\ точки\ на\ прямых,\ }\]
\[\mathbf{перпендикулярных\ }\]
\[\mathbf{поверхности\ зеркала.\ }\]
\[\mathbf{Если\ три\ шарика\ расставлены\ }\]
\[\mathbf{вдоль\ прямой,\ }\]
\[\mathbf{перпендикулярной\ }\]
\[\mathbf{поверхности\ зеркала,\ то\ их\ }\]
\[\mathbf{зеркальные\ отражения\ }\]
\[\mathbf{располагаются\ в\ обратном\ }\]
\[\mathbf{порядке.\ \ }\]
\[\mathbf{Если\ вы\ стоите\ на\ зеркальном\ }\]
\[\mathbf{полу,\ то\ ваша\ ось\ }\text{верх\ -\ низ}\]
\[\mathbf{перпендикулярна\ плоскости\ }\]
\[\mathbf{зеркала\ и\ при\ отражении\ перед\ }\]
\[\mathbf{остается\ передом,\ левая\ }\]
\[\mathbf{сторона\ - \ левой\ стороной,\ но\ }\]
\[\mathbf{голова\ оказывается\ }\]
\[\mathbf{обращенной\ вниз,\ а\ ноги\ - \ }\]
\[\mathbf{вверх.}\]
\[\mathbf{Если\ вы\ стоите\ боком\ к\ }\]
\[\mathbf{зеркалу,\ то\ ваша\ ось\ }\]
\[\text{право\ -\ лево\ }\mathbf{перпендикулярна\ }\]
\[\mathbf{его\ поверхности.\ }\]
\[\mathbf{При\ отражении\ в\ зеркале\ }\]
\[\mathbf{голова\ останется\ вверху,\ }\]
\[\mathbf{ноги\ - \ внизу,\ перед\ }\]
\[\mathbf{останется\ передом,\ но\ правая\ и\ }\]
\[\mathbf{левая\ стороны\ поменяются\ }\]
\[\mathbf{местами.}\]
24
\[\boxed{\mathbf{24.}}\]
\[1)\ Прямоугольный\ лист\ бумаги\ \]
\[разедлим\ пополам\ по\ длине.\]
\[2)\ Теперь\ разделим\ на\ 4\ части\ \]
\[по\ ширине.\]
\[3)\ Разрежем\ в\ трех\ местах.\]

\[4)\ Поднимем\ среднюю\ часть\ \]
\[справа.\]

\[5)\ Перевернем\ одну\ из\ нижних\ \]
\[частей\ по\ разрезу.\]

\[6)\ Сложим\ фигуру\ вверху\ и\ \]
\[сделаем\ заломы\ по\ бокам,\ \]
\[чтобы\ она\ стояла.\]

