Решебник по геометрии 10 класс Атанасян ФГОС Задачи для подготовки к ЕГЭ

Задание 3

\[\boxed{\mathbf{Задание\ 3.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[S = \frac{1}{2} \cdot 4 \cdot 5 = 10\ см^{2}\text{.\ }\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{2.}}\]

\[Достроим\ треугольник\ до\ \]

\[прямоугольного:\]

\[Получим:\]

\[S = \frac{1}{2} \cdot 4 \cdot 4 - \frac{1}{2} \cdot 4 \cdot 1 = 8 - 2 =\]

\[= 6\ см^{2}.\]

\[Ответ:6\ см^{2}.\]

\[\boxed{\mathbf{3.}}\]

\[Достроим\ треугольник\ до\ \]

\[прямоугольника:\]

\[Получим:\]

\[S =\]

\[= 6 \cdot 4 - \frac{1}{2} \cdot 4 \cdot 2 - \frac{1}{2} \cdot 4 \cdot 2 - \frac{1}{2} \cdot 6 \cdot 2 =\]

\[= 24 - 4 - 4 - 6 = 10\ см^{2}.\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{4.}}\]

\[Достроим:\]

\[Получим:\]

\[Ответ:5,5\ см^{2}.\]

\[\boxed{\mathbf{5.}}\]

\[Разобьем\ на\ две\ фигуры:\]

\[Получим:\]

\[S = \frac{1}{2} \cdot 2 \cdot 3 + 3 \cdot 3 = 3 + 9 =\]

\[= 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{6.}}\]

\[Разобьем\ на\ три\ фигуры:\]

\[S = \frac{1}{2} \cdot 3 \cdot 1 + 2 \cdot 3 + \frac{1}{2} \cdot 3 \cdot 3 =\]

\[= 6 + 1,5 + 4,5 = 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{7.}}\]

\[Разобьем\ на\ три\ фигуры:\]

\[S = \frac{1}{2} \cdot 4 \cdot 1 + 4 \cdot 2 + \frac{1}{2} \cdot 2 \cdot 4 =\]

\[= 2 + 8 + 4 = 14\ см^{2}.\]

\[Ответ:14\ см^{2}.\]

\[\boxed{\mathbf{8.}}\]

\[Дополним:\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{9.}}\]

\[Дополним:\]

\[S = 4 \cdot 4 - 4 \cdot \frac{1}{2} \cdot 3 \cdot 1 =\]

\[= 16 - 6 = 10\ см^{2}.\]

\[Ответ:10\ см^{2}.\]

\[\boxed{\mathbf{10.}}\]

\[\angle AOB = 90{^\circ}:\]

\[\cup ACB = 360{^\circ} - 90{^\circ} = 270{^\circ}.\]

\[S = \frac{270{^\circ}}{360{^\circ}} \cdot S_{кр} = \frac{3}{4}\pi R^{2}.\]

\[R = OC = 4\ см.\]

\[\frac{S}{\pi} = \frac{3}{4}R^{2} = \frac{3}{4} \cdot 4^{2} = 12\ см^{2}.\]

\[Ответ:12\ см^{2}.\]

\[\boxed{\mathbf{11.}}\]

\[S = a^{2} = 2\]

\[a = \sqrt{2}:\]

\[d = \sqrt{\left( \sqrt{2} \right)^{2} + \left( \sqrt{2} \right)^{2}} = \sqrt{2 + 2} =\]

\[= 2.\]

\[Ответ:диагональ\ равна\ 2.\]

\[\boxed{\mathbf{12.}}\]

\[a = 8;\ \ b = 12;\ \ \]

\[\angle(a;b) = 150{^\circ}.\]

\[S = \frac{1}{2}ab \cdot \sin{150{^\circ}} =\]

\[= \frac{1}{2} \cdot 8 \cdot 12 \cdot \sin{30{^\circ}} = 48 \cdot \frac{1}{2} =\]

\[= 24.\]

\[Ответ:24.\]

\[\boxed{\mathbf{13.}}\]

\[a = 6;\ \ b = 8;\]

\[\angle(a;b) = 30{^\circ}.\]

\[S = a \cdot b \cdot \sin{30{^\circ}} = 6 \cdot 8 \cdot \frac{1}{2} =\]

\[= 24.\]

\[Ответ:24.\]

\[\boxed{\mathbf{14.}}\]

\[S = 12;\ \ a = 6.\]

\[S = \frac{1}{2}a \cdot b = 12\]

\[\frac{1}{2} \cdot 6 \cdot b = 12\]

\[b = 12\ :3\]

\[b = 4.\]

\[Ответ:второй\ катет\ равен\ 4.\]

\[\boxed{\mathbf{15.}}\]

\[a = 3;\ \ b = 1;\ \ h = 1:\]

\[S = \frac{a + b}{2} \cdot h = \frac{3 + 1}{2} \cdot 1 = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{16.}}\]

\[P_{1}\ :P_{2} = 3\ :5\]

\[S_{1} = 36.\]

\[Отношение\ периметров:\]

\[k = \frac{3}{5}.\]

\[Отношение\ площадей:\]

\[\frac{S_{1}}{S_{2}} = k^{2} = \frac{9}{25};\]

\[S_{2} = 36 \cdot \frac{25}{9} = 100.\]

\[Ответ:100.\]

\[\boxed{\mathbf{17.}}\]

\[C = \sqrt{\pi}.\]

\[Длина\ окружности:\]

\[C = 2\pi R\]

\[R = \frac{C}{2\pi} = \frac{\sqrt{\pi}}{2\pi} = \frac{1}{2\sqrt{\pi}}.\]

\[Площадь\ круга:\]

\[S = \pi R^{2} = \pi \cdot \left( \frac{1}{2\sqrt{\pi}} \right)^{2} = \pi \cdot \frac{1}{4\pi} =\]

\[= \frac{1}{4} = 0,25.\]

\[Ответ:0,25.\]

\[\boxed{\mathbf{18.}}\]

\[R = 1;\ \ C_{\cup} = 2.\]

\[C_{\cup} = \frac{\alpha}{2\pi} \cdot 2\pi R = \alpha R;\]

\[\alpha = \frac{C_{\cup}}{R};\]

\[\alpha - центральный\ угол\ в\ \]

\[радианах.\]

\[Площадь\ сектора:\]

\[S = \frac{\alpha}{2\pi} \cdot \pi R^{2} = \frac{\alpha R^{2}}{2} = \frac{C_{\cup}}{R} \cdot \frac{R^{2}}{2} =\]

\[= \frac{C_{\cup} \cdot R}{2} = \frac{2 \cdot 1}{2} = 1.\]

\[Ответ:1.\]

\[\boxed{\mathbf{19.}}\]

\[Пусть\ x - одна\ сторона\ \]

\[прямоугольника;\]

\[(x - 2) - другая\ сторона.\]

\[Известно,\ что\ периметр\ \]

\[равен\ 16.\]

\[Составим\ уравнение:\]

\[2 \cdot (x + x - 2) = 16\]

\[2x - 2 = 8\]

\[2x = 10\]

\[x = 5\ (см) - одна\ сторона\ \]

\[прямоугольника.\]

\[x - 2 = 5 - 2 = 3\ (см) - другая\ \]

\[сторона.\]

\[S = 5 \cdot 3 = 15\ см^{2}.\]

\[Ответ:15\ см^{2}.\]

\[\boxed{\mathbf{20.}}\]

\[34\ :2 = 17 - сумма\ длин\ двух\ \]

\[сторон.\]

\[Пусть\ x - одна\ сторона\ \]

\[прямоугольника;\]

\[(17 - x) - другая\ сторона.\]

\[Площадь\ равна\ 60.\]

\[Составим\ уравнение:\]

\[x(17 - x) = 60\]

\[17x - x^{2} - 60 = 0\]

\[x^{2} - 17x + 60 = 0\]

\[x_{1} + x_{2} = 17;\ \ \ x_{1} \cdot x_{2} = 60\]

\[x_{1} = 12;\ \ \ x_{2} = 5.\]

\[12\ и\ 5 - стороны\ \]

\[прямоугольника.\]

\[По\ теореме\ Пифагора\ найдем\ \]

\[его\ диагональ:\]

\[d = \sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} =\]

\[= \sqrt{169} = 13.\]

\[Ответ:13.\]

\[\boxed{\mathbf{21.}}\]

\[a = 9;\ \ b = 15;\]

\[h_{a} = 10;\ \ h_{b} - ?\]

\[S = a \cdot h_{a} = b \cdot h_{b}\]

\[9 \cdot 10 = 15 \cdot h_{b}\]

\[h_{b} = 90\ :15\]

\[h_{b} = 6.\]

\[Ответ:6.\]

\[\boxed{\mathbf{22.}}\]

\[P = 12;\ \ r = 1.\]

\[S = \frac{1}{2} \cdot P \cdot r = \frac{1}{2} \cdot 12 \cdot 1 = 6.\]

\[Ответ:6.\]

\[\boxed{\mathbf{23.}}\]

\[a = 2;\ \ b = 8;\ \ S = 30.\]

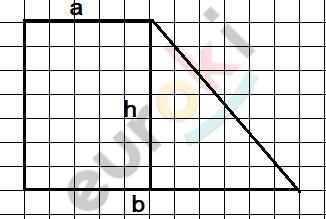
\[S = \frac{a + b}{2} \cdot h\]

\[h = \frac{2S}{a + b} = \frac{2 \cdot 30}{8 + 2} = 6.\]

\[b - a = 8 - 2 = 6;\]

\[h = b - a:\]

\[получившися\ \mathrm{\Delta} -\]

\[равнобедренный.\]

\[Значит,\ острый\ угол\ \alpha:\]

\[\alpha = 90{^\circ}\ :2 = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{24.}}\]

\[A(5;9).\]

\[При\ симметрии\ относительно\ \]

\[Oy:\]

\[A_{1}( - 5;9)\text{.\ }\]

\[Ответ:x_{1} = - 5.\]

\[\boxed{\mathbf{25.}}\]

\[A(3;7);\ \ B( - 1;3).\]

\[Ордината\ середины\ отрезка:\]

\[y = \frac{7 + 3}{2} = 5.\]

\[Ответ:y = 5.\]

\[\boxed{\mathbf{26.}}\]

\[\overrightarrow{a}\left\{ 6;8 \right\}:\]

\[\left| \overrightarrow{a} \right| = \sqrt{6^{2} + 8^{2}} = \sqrt{100} = 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{27.}}\]

\[A(3;0);\ \ B(0;3):\]

\[\frac{x - 3}{0 - 3} = \frac{y - 0}{3 - 0}\]

\[- (x - 3) = y\]

\[Уравнение\ прямой:\]

\[y = - x + 3.\]

\[k = - 1.\]

\[Ответ:\ - 1.\]

\[\boxed{\mathbf{28.}}\]

\[O(0;0);A(8;6);B(12; - 2).\]

\[\overrightarrow{\text{BO}} = \overrightarrow{\text{AC}} = \overrightarrow{a}\]

\[\overrightarrow{\text{BO}} = \left\{ 0 - 12;0 + 2 \right\} = \left\{ - 12;2 \right\}.\]

\[a_{x} = - 12;\ \ a_{y} = 2.\]

\[x_{C} = x_{A} + a_{x} = 8 - 12 = - 4;\]

\[y_{C} = y_{A} + a_{y} = 6 + 2 = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{29.}}\]

\[3x + 2y = 6;\ \ при\ y = 0:\]

\[3x + 2 \cdot 0 = 6\]

\[3x = 6\]

\[x = 2.\]

\[Ответ:x = 2.\]

\[\boxed{\mathbf{30.}}\]

\[3x + 2y = 6;\ \ y = - x:\]

\[2y = 6 - 3x\]

\[y = 3 - 1,5x.\]

\[Получаем:\]

\[3 - 1,5x = - x\]

\[0,5x = 3\]

\[x = 6.\]

\[y = - x = - 6.\]

\[Ответ:\ - 6.\]

\[\boxed{\mathbf{31.}}\]

\[P(5;7) - центр\ окружности.\]

\[r\bot Ox:\]

\[x = x_{P} = 7.\]

\[(7;0) - точка\ касания\ оси\ \text{Ox.}\]

\[Найдем\ радиус\ окружности:\]

\[r = \sqrt{(7 - 7)^{2} + (5 - 0)^{2}} =\]

\[= \sqrt{25} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{32.}}\]

\[⊿ABC;\ \ \]

\[A(6;0);B(0;10);C(6;10).\]

\[P\left( x_{p};y_{p} \right) - центр\ описанной\ \]

\[окружности.\]

\[\overrightarrow{\text{CA}} = \left\{ 6 - 6;10 - 0 \right\} = \left\{ 0;10 \right\};\]

\[\overrightarrow{\text{CB}} = \left\{ 0 - 6;10 - 10 \right\} = \left\{ - 6;0 \right\};\]

\[\overrightarrow{\text{CA}} \cdot \overrightarrow{\text{CB}} = 0 \cdot ( - 6) + 10 \cdot 0 = 0.\]

\[\overrightarrow{\text{CA}}\bot\overrightarrow{\text{CB}}:\]

\[⊿\text{ABC} - прямоугольный;\]

\[центр\ описанной\ окружности -\]

\[середина\ гипотенузы\ \text{AB.}\]

\[x_{p} = \frac{6 + 0}{2} = 3;\ \ \ y_{p} = \frac{0 + 10}{2} =\]

\[= 5.\]

\[Ответ:3.\]

\[\boxed{\mathbf{33.}}\]

\[⊿ABC;\ \ \]

\[A(1;1);B(4;3);C(4;5).\]

\[Достроим:\]

\[Получим:\]

\[S = \frac{1}{2} \cdot 3 \cdot 4 - \frac{1}{2} \cdot 2 \cdot 3 = 6 - 3 =\]

\[= 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{34.}}\]

\[ABCD - прямоугольник;\]

\[AB = 6;\ \ AD = 8.\]

\[По\ правилу\ параллелограмма:\]

\[\overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} = \overrightarrow{\text{AC}}.\]

\[Длина\ суммы\ векторов\ равна\ \]

\[длине\ диагонали:\]

\[\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} \right| = \left| \overrightarrow{\text{AC}} \right| = AC =\]

\[= \sqrt{AB^{2} + AD^{2}} = \sqrt{6^{2} + 8^{2}} =\]

\[= 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{35.}}\]

\[ABCD - ромб;\]

\[AC = 12;\ \ BD = 16.\]

\[\overrightarrow{\text{AB}} = \overrightarrow{\text{AO}} + \overrightarrow{\text{OB}}\]

\[Диагонали\ ромба\ \]

\[перпендикулярны\ и\ в\ точке\ \]

\[пересечения\ делятся\ пополам:\]

\[AO = \frac{\text{AC}}{2} = \frac{12}{2} = 6;\ \ \ \]

\[OB = \frac{\text{BD}}{2} = \frac{16}{2} = 8.\]

\[\left( \overrightarrow{\text{AB}} \right)^{2} =\]

\[= \left( \overrightarrow{\text{AO}} \right)^{2} + \left( \overrightarrow{\text{OB}} \right)^{2} + 2\overrightarrow{\text{AO}} \cdot \overrightarrow{\text{OB}} =\]

\[= AO^{2} + OB^{2} + 2AO \cdot OB \cdot \cos{90{^\circ}} =\]

\[= AO^{2} + OB^{2} = 6^{2} + 8^{2} = 10^{2}\]

\[\left| \overrightarrow{\text{AB}} \right| = 10.\]

\[Ответ:10.\]

\[\boxed{\mathbf{36.}}\]

\[ABCD - ромб;\]

\[AC = 12;BD = 16.\]

\[Диагонали\ ромба\ \]

\[перпендикулярны\ и\ в\ точке\ \]

\[пересечения\ делятся\ пополам:\]

\[AO = \frac{\text{AC}}{2} = \frac{12}{2} = 6;\ \ \]

\[BO = \frac{\text{BD}}{2} = \frac{16}{2} = 8.\]

\[\overrightarrow{\text{BO}} = \overrightarrow{\text{OD}};\]

\[\angle\left( \overrightarrow{\text{AO}};\overrightarrow{\text{BO}} \right) = \angle\left( \overrightarrow{\text{AO}};\overrightarrow{\text{OD}} \right) = 90{^\circ};\]

\[\overrightarrow{\text{AO}} \cdot \overrightarrow{\text{BO}} = AO \cdot BO \cdot \cos{90{^\circ}} = 0.\]

\[Ответ:0.\]

\[\boxed{\mathbf{37.}}\]

\[⊿ABC - равносторонний;\]

\[AB = \sqrt{3}.\]

\[Проведем\ \overrightarrow{\text{CD}} = \overrightarrow{\text{AB}}:\]

\[ACDB - параллелограмм.\]

\[По\ правилу\ параллелограмма:\]

\[\overrightarrow{\text{AB}} + \overrightarrow{\text{AC}} = \overrightarrow{\text{AC}} + \overrightarrow{\text{CD}} = \overrightarrow{\text{AD}}\]

\[\left| \overrightarrow{\text{AB}} + \overrightarrow{\text{AC}} \right| = \left| \overrightarrow{\text{AD}} \right| = AD;\]

\[\angle ACD = 180{^\circ} - \angle A = 120{^\circ};\]

\[\cos{120{^\circ}} = - \cos(180{^\circ} - 120{^\circ}) =\]

\[= - \cos{60{^\circ}} = - \frac{1}{2}.\]

\[По\ теореме\ косинусов:\]

\[AD^{2} =\]

\[= AC^{2} + CD^{2} - 2AC \cdot CD \cdot \cos{\angle ACD} =\]

\[= \left( \sqrt{3} \right)^{2} + \left( \sqrt{3} \right)^{2} - 2\sqrt{3} \cdot \sqrt{3} \cdot \left( - \frac{1}{2} \right) =\]

\[= 9\]

\[AD = \sqrt{9} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{38.}}\]

\[⊿ABC - равносторонний;\]

\[AB = 1.\]

\[Решение.\]

\[Все\ углы\ ⊿\text{ABC}\ равны\ 60{^\circ}.\]

\[\overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AC}} = AB \cdot AC \cdot \cos{60{^\circ}} =\]

\[= 1 \cdot 1 \cdot \frac{1}{2} = \frac{1}{2} = 0,5.\]

\[Ответ:0,5.\]

Задание 6

\[\boxed{\mathbf{Задание\ 6.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \sin A = \frac{7}{25}\]

\[\sin B = \sin(90{^\circ} - A) = \cos A =\]

\[= \sqrt{1 - \sin^{2}A} = \sqrt{1 - \left( \frac{7}{25} \right)^{2}\ } =\]

\[= \frac{\sqrt{25^{2} - 7^{2}}}{25} = \frac{\sqrt{18 \cdot 32}}{25} =\]

\[= \frac{\sqrt{36 \cdot 16}}{25} = \frac{24}{25}.\]

\[Ответ:\ \frac{24}{25}.\]

\[\boxed{\mathbf{2.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};BC = 6;\]

\[tg\ A = 0,5.\]

\[AC = AB \cdot \cos A;\ \ \]

\[BC = AC \cdot \sin A;\]

\[\frac{\text{BC}}{\text{AC}} = tg\ A\]

\[AC = \frac{\text{BC}}{\text{tg\ A}} = \frac{6}{0,5} = 12.\]

\[Ответ:12.\]

\[\boxed{\mathbf{3.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ AB = 13;\]

\[tg\ A = 0,2 = \frac{1}{5};\]

\[CH - высота.\]

\[⊿ACB\ и\ ⊿AHC - подобны\ по\]

\[двум\ углам:\]

\[\angle ACB = \angle AHC = 90{^\circ};\]

\[\angle A - общий.\]

\[Отсюда:\]

\[\frac{\text{AB}}{\text{AC}} = \frac{\text{BC}}{\text{CH}}\]

\[CH = \frac{AC \cdot BC}{\text{AB}} =\]

\[= \frac{AB \cdot \cos A \cdot AB \cdot \sin A}{\text{AB}} =\]

\[= \frac{AB \cdot \sin{2A}}{2}.\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} = \frac{1}{\sqrt{1 + \frac{1}{25}}} =\]

\[= \frac{5}{\sqrt{26}};\]

\[\sin A = \cos A \cdot tg\ A = \frac{5}{\sqrt{26}} \cdot \frac{1}{5} =\]

\[= \frac{1}{\sqrt{26}};\]

\[\sin{2A} = 2\sin A\cos A =\]

\[= 2 \cdot \frac{1}{\sqrt{26}} \cdot \frac{5}{\sqrt{26}} = \frac{10}{26} = \frac{5}{13}.\]

\[Получаем:\]

\[CH = \frac{13 \cdot \frac{5}{13}}{2} = 2,5.\]

\[Ответ:2,5.\]

\[\boxed{\mathbf{4.}}\]

\[Дано:\]

\[⊿ABC;\]

\[AC = BC;\]

\[AB = 9,6;\]

\[\sin A = \frac{7}{25}.\]

\[Решение.\]

\[1)\ Построим\ CH\bot AB.\]

\[2)\ ⊿ABC - равнобедренный:\]

\[CH - высота,\ медиана\ и\ \]

\[биссектриса.\]

\[AH = \frac{1}{2}AB = 4,8;\ \ \ \]

\[AH = AC \cdot \cos A\]

\[AC = \frac{\text{AH}}{\cos A};\]

\[\cos A = \sqrt{1 - \sin^{2}A} =\]

\[= \sqrt{1 - \frac{49}{625}} = \frac{24}{25} = \frac{96}{100} = 0,96;\]

\[AC = \frac{4,8}{0,96} = \frac{480}{96} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{5.}}\]

\[⊿ABC;AC = BC = 25;\ \ AB = 40.\]

\[CH - высота,\ медиана\ и\ \]

\[биссектриса:\]

\[AH = \frac{1}{2}AB = 20.\]

\[\cos A = \frac{\text{AH}}{\text{AC}} = \frac{20}{25} = \frac{4}{5};\]

\[\sin A = \sqrt{1 - \cos^{2}A} = \sqrt{1 - \frac{16}{25}} =\]

\[= \sqrt{\frac{9}{25}} = \frac{3}{5} = 0,6.\]

\[Ответ:0,6.\]

\[\boxed{\mathbf{6.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ BH = 24;\]

\[CH = 7 - высота.\]

\[⊿ACB\ и\ ⊿CHB - подобны\ по\ \]

\[двум\ углам:\]

\[\angle ACB = \angle CHB = 90{^\circ};\]

\[\angle C - общий.\]

\[Отсюда:\]

\[\frac{\text{AC}}{\text{CH}} = \frac{\text{BC}}{\text{BH}}\]

\[\frac{\text{BC}}{\text{AC}} = \frac{\text{BH}}{\text{CH}}\]

\[\frac{\text{BC}}{\text{AC}} = tg\ A = \frac{24}{7};\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} =\]

\[= \frac{1}{\sqrt{1 + \left( \frac{24}{7} \right)^{2}}} = \frac{7}{\sqrt{7^{2} + 24^{2}}} =\]

\[= \frac{7}{\sqrt{625}} = \frac{7}{25} = \frac{28}{100} = 0,28.\]

\[Ответ:0,28.\]

\[\boxed{\mathbf{7.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};tg\ A = \frac{24}{7};\]

\[\angle DBA - внешний\ угол\ при\ \]

\[вершине\ \text{B.}\]

\[\cos{\angle DBA} = \cos(180{^\circ} - B) =\]

\[= - \cos B = - \cos(90{^\circ} - A) =\]

\[= - \sin A;\]

\[\cos A = \frac{1}{\sqrt{1 + tg^{2}A}} =\]

\[= \frac{1}{\sqrt{1 + \left( \frac{24}{7} \right)^{2}\ }} = \frac{7}{\sqrt{7^{2} + 24^{2}}} =\]

\[= \frac{7}{\sqrt{625}} = \frac{7}{25};\]

\[\sin A = \cos A \cdot tg\ A = \frac{7}{25} \cdot \frac{24}{7} =\]

\[= \frac{24}{25} = \frac{96}{100} = 0,96;\]

\[\cos{\angle DBA} = - 0,96.\]

\[Ответ:\ - 0,96.\]

\[\boxed{\mathbf{8.}}\]

\[ABCD - параллелограмм;\ \]

\[{\cos A = \frac{\sqrt{51}}{10}: }{Сумма\ смежных\ углов:}\]

\[\angle A + \angle B = 180{^\circ}\]

\[\sin B = \sin(180{^\circ} - A) = \sin A =\]

\[= \sqrt{1 - \cos^{2}A} =\]

\[= \sqrt{1 - \left( \frac{\sqrt{51}}{10} \right)^{2}} = \sqrt{\frac{49}{100}} = \frac{7}{10} =\]

\[= 0,7.\]

\[Ответ:0,7.\]

\[\boxed{\mathbf{9.}}\]

\[ABCD - трапеция;BC \parallel AD;\ \]

\[BC = 31;AD = 45;\]

\[AB = CD = 25.\]

\[Построим\ высоты:\]

\[BE\bot AD;\ \ CF\bot AD.\]

\[EBCF - прямоугольник.\]

\[EF = BC = 31.\]

\[⊿AEB = ⊿DFC - по\ гипотенузе\ \]

\[и\ катету:\]

\[BE = CF;\]

\[AB = CD.\]

\[Отсюда:\]

\[AE = FD = \frac{AD - EF}{2} =\]

\[= \frac{45 - 31}{2} = 7;\]

\[\cos A = \frac{\text{AE}}{\text{AB}} = \frac{7}{25};\]

\[\sin A = \sqrt{1 - \cos^{2}A} =\]

\[= \sqrt{1 - \left( \frac{7}{25} \right)^{2}} = \frac{24}{25} = 0,96.\]

\[Ответ:0,96.\]

\[\boxed{\mathbf{10.}}\]

\[ABCD - трапеция;BC \parallel AD;\ \]

\[BC = 6;AD = 12;AB = CD;\]

\[\sin A = 0,8.\]

\[Построим\ высоты:\]

\[BE\bot AD;\ \ CF\bot AD.\]

\[EBCF - прямоугольник.\]

\[EF = BC = 31.\]

\[⊿AEB = ⊿DFC - по\ гипотенузе\ \]

\[и\ катету:\]

\[BE = CF;\]

\[AB = CD.\]

\[Отсюда:\]

\[AE = FD = \frac{AD - EF}{2} =\]

\[= \frac{12 - 6}{2} = 3;\]

\[AB = \frac{\text{AE}}{\cos A}\]

\[\cos A = \sqrt{1 - sin^{2}A} =\]

\[= \sqrt{1 - {0,8}^{2}} = 0,6.\]

\[AB = \frac{3}{0,6} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{11.}}\]

\[Достроим\ угол\ до\ \]

\[прямоугольника.\]

\[OA = 4;\]

\[OB = \sqrt{2^{2} + 4^{2}} = 2\sqrt{5};\]

\[AB = \sqrt{6^{2} + 4^{2}} = 2\sqrt{13}.\]

\[По\ теореме\ косинусов:\]

\[\cos O = \frac{OA^{2} + OB^{2} - AB^{2}}{2OA \cdot OB} =\]

\[= \frac{4^{2} + \left( 2\sqrt{5} \right)^{2} - \left( 2\sqrt{13} \right)^{2}}{2 \cdot 4 \cdot 2\sqrt{5}} =\]

\[= \frac{16 + 20 - 52}{16\sqrt{5}} = - \frac{1}{\sqrt{5}};\ - \ совьника.до\ \ ндикулярны\ и\ в\ енузы\ \]

\[\sin O = \sqrt{1 - \cos^{2}O} =\]

\[= \sqrt{1 - \left( - \frac{1}{\sqrt{5}} \right)^{2}} = \sqrt{1 - \frac{1}{5}} =\]

\[= \sqrt{\frac{4}{5}} = \frac{2}{\sqrt{5}};\ \]

\[\sqrt{5} \cdot \sin O = \sqrt{5} \cdot \frac{2}{\sqrt{5}} = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{12.}}\]

\[\mathrm{\Delta}ABC;AB = BC;\ \ \angle 1 = 98{^\circ}.\]

\[Сумма\ углов\ треугольника\ \]

\[равна\ 180{^\circ};\]

\[2 \cdot 98{^\circ} = 196{^\circ} > 180{^\circ}.\]

\[Значит:\]

\[\angle 1 = 98{^\circ} - угол\ при\ вершине.\]

\[Углы\ при\ основании:\]

\[\angle 2 = \angle 3 = (180{^\circ} - 98{^\circ})\ :2 =\]

\[= 41{^\circ}.\]

\[Ответ:41{^\circ}.\]

\[\boxed{\mathbf{13.}}\]

\[⊿ABC;\ \ \]

\[AD - биссектриса;\ \ \angle C = 30{^\circ};\ \ \]

\[\angle BAD = 18{^\circ}.\]

\[AD - биссектриса:\]

\[\angle CAD = \angle BAD = 18{^\circ}.\]

\[\angle ADB - внешний\ при\ вершине\ \]

\[\text{D\ }\left( для\ ⊿\text{ACD} \right):\]

\[\angle ADB = \angle CAD + \angle C =\]

\[= 18{^\circ} + 30{^\circ} = 48{^\circ}.\]

\[Ответ:48{^\circ}.\]

\[\boxed{\mathbf{14.}}\]

\[⊿ABC;\ \ \angle A = 58{^\circ};\ \angle B = 72{^\circ};\]

\[AA_{1};\ \ BB_{1} - высоты;\]

\[O - точка\ пересечения\ высот.\]

\[В\ треугольнике\ ABC:\]

\[\angle C = 180{^\circ} - (\angle A + \angle B) =\]

\[= 180{^\circ} - (58{^\circ} + 72{^\circ}) = 50{^\circ}.\]

\[В\ четырехугольнике\ OA_{1}CB_{1}:\]

\[\angle A_{1}OB_{1} =\]

\[= 360{^\circ} - (\angle C + 2 \cdot 90{^\circ}) =\]

\[= 360{^\circ} - 230{^\circ} = 130{^\circ}.\]

\[Ответ:130{^\circ}.\]

\[\boxed{\mathbf{15.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \]

\[AA_{1};\ \ BB_{1} - биссектрисы;\]

\[O - точка\ пересечения\ \]

\[биссектрис.\]

\[Пусть\ \angle A = \alpha;\]

\[\angle B = 90{^\circ} - \alpha.\]

\[\angle AOB_{1} - внешний\ угол\ при\ \]

\[вершине\ \text{O\ }\left( для\ ⊿\text{AOB} \right):\]

\[\angle AOB_{1} = \angle OAB + \angle OBA =\]

\[= \frac{\alpha}{2} + \frac{90{^\circ} - \alpha}{2} = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{16.}}\]

\[⊿ABC;\ \ \angle C = 90{^\circ};\ \ \angle B > \angle A;\]

\[CH - высота;\]

\[CM - медиана;\]

\[\angle MCH = 20{^\circ}.\]

\[Пусть\ \angle A = \alpha;\ \ \angle B = 90{^\circ} - \alpha:\]

\[\angle BCH = 90{^\circ} - \angle B = \alpha;\]

\[\angle MCA =\]

\[= 90{^\circ} - (\angle MCH + \angle BCH) =\]

\[= 90{^\circ} - (20{^\circ} + \alpha) = 70{^\circ} - \alpha.\]

\[Точка\ M - центр\ вписанной\ \]

\[окружности:\]

\[MA = MC.\]

\[⊿AMC - равнобедренный\ с\ \]

\[основанием\ AC:\]

\[\angle A = \angle MCA.\]

\[Получаем:\]

\[\alpha = 70 - \alpha\]

\[2\alpha = 70\]

\[\alpha = 35{^\circ}.\]

\[\angle B = 90{^\circ} - \alpha = 90{^\circ} - 35{^\circ} = 55{^\circ}.\]

\[Ответ:55{^\circ}.\]

\[\boxed{\mathbf{17.}}\]

\[ABCD - ромб;AB = 2\sqrt{3};\ \ \]

\[\angle A = 60{^\circ};\]

\[AH - высота.\]

\[AD \parallel BC;AB - секущая:\]

\[\angle HBA = \angle A = 60{^\circ} - как\ \]

\[накрест\ лежащие.\]

\[В\ треугольнике\ AHB:\]

\[AH = AB \cdot \sin{\angle HBA} =\]

\[= 2\sqrt{3} \cdot \frac{\sqrt{3}}{2} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{18.}}\]

\[ABCD - трапеция;AD \parallel BC;\]

\[AD = 10;BC = 4;\]

\[KM - средняя\ линия.\]

\[1)\ AK = BK;\ \ KE \parallel BC:\]

\[KE - средняя\ линия\ ⊿ABC;\]

\[KE = \frac{1}{2}BC = 2.\]

\[2)\ Аналогично:\ \ \]

\[KF - средняя\ линия\ ⊿ABD;\]

\[KF = \frac{1}{2}AD = 5.\]

\[EM - средняя\ линия\ ⊿ACD:\]

\[EM = \frac{1}{2}AD = 5.\]

\[FM - средняя\ линия\ ⊿BCD:\]

\[FM = \frac{1}{2}BC = 2.\]

\[3)\ Получаем:\]

\[\max(KF;FM;KE;EM) =\]

\[= \max(5;2;2;5) = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{19.}}\]

\[ABCD - трапеция;\ \ AD \parallel BC;\ \ \]

\[AD > BC;\]

\[AD = CD;\ \ AC\bot BD;\]

\[BH = 18 - высота;\]

\[KM - средняя\ линия.\]

\[1)\ ⊿ABD = ⊿DCA - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[AB = CD;\]

\[AD - общая;\]

\[\angle A = \angle D.\]

\[Отсюда:\]

\[\angle BDA = \angle CAD.\]

\[2)\ O - точка\ пересечения\ \]

\[диагоналей\ \text{AC\ }и\ \text{BD.}\]

\[В\ ⊿AOD\ углы\ при\ основании\ \]

\[равны,\ а\ угол\ при\ вершине -\]

\[прямой:\]

\[\angle ODA = \angle OAD = 45{^\circ}.\]

\[3)\ В\ треугольнике\ BHD:\]

\[\angle BHD = 90{^\circ};\]

\[\angle BDH = 45{^\circ};\]

\[\angle DBH = 90 - 45 = 45{^\circ}.\]

\[⊿BHD - прямоугольный\ и\ \]

\[равнобедренный:\]

\[BH = HD.\]

\[4)\ ⊿AHB - прямоугольный:\]

\[середина\ гипотенузы\ K -\]

\[центр\ описанной\ окружности;\]

\[KA = KH = \frac{1}{2}AB = MD.\]

\[5)\ KM \parallel HD;\ \ KH = MD:\]

\[HKMD - параллелограмм;\]

\[HD = KM.\]

\[6)\ Получаем:\]

\[BH = HD = KM;\]

\[KM = 18.\]

\[Ответ:18.\]

\[\boxed{\mathbf{20.}}\]

\[Окружность\ (O;r);\ \]

\[AB - хорда;\ \ AB = r;\]

\[\angle ACB - вписанный.\]

\[⊿AOB - равносторонний:\]

\[AB = OA = OB = r.\]

\[\angle AOB = 60{^\circ} - центральный,\ \]

\[на\ хорде\ \text{AB.}\]

\[\angle ACB - вписан\ на\ хорде\ AB:\]

\[\angle ACB = \frac{1}{2}\angle AOB = \frac{1}{2} \cdot 60 = 30{^\circ}.\]

\[Ответ:30{^\circ}.\]

\[\boxed{\mathbf{21.}}\]

\[Окружность\ (O;R);\]

\[ABCD - вписанный\ \]

\[четырехугольник;\]

\[\angle A = 54{^\circ}.\]

\[Решение.\]

\[У\ вписанного\ \]

\[четырехугольника\ сумма\ \]

\[противоположных\ углов\ равна\ \]

\[180{^\circ}:\]

\[\angle C = 180{^\circ} - 54{^\circ} = 126{^\circ}.\]

\[Ответ:126{^\circ}.\]

\[\boxed{\mathbf{22.}}\]

\[⊿ABC - правильный;\ \ AB = \sqrt{3};\]

\[(O;r) - вписанная\ окружность.\]

\[Решение.\]

\[В\ правильном\ треугольнике\ \]

\[центр\ вписанной\ окружности\ \]

\[совпадает\ с\ центром\ \]

\[треугольника.\]

\[O - точка\ пересечения\ медиан,\ \]

\[биссектрис\ и\ высот.\]

\[r = OA_{1} = \frac{1}{3}AA_{1} =\]

\[= \frac{1}{3}AB \cdot \sin{60{^\circ}} = \frac{1}{3} \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2} =\]

\[= \frac{3}{6} = \frac{1}{2} = 0,5.\]

\[Ответ:0,5.\]

\[\boxed{\mathbf{23.}}\]

\[ABCDEF - правильный\ \]

\[шестиугольник;AB = \sqrt{3};\]

\[(O;r) - вписанная\ окружность.\]

\[Решение.\]

\[В\ правильном\ шестиугольнике\ \]

\[центр\ вписанной\ окружности\ \]

\[совпадает\ с\ центром\ \]

\[шестиугольника.\]

\[⊿AOB - правильный:\]

\[OA = OB = AB;\]

\[OH\bot AB - высота.\]

\[r = OH = AB \cdot \sin{60{^\circ}} =\]

\[= \sqrt{3} \cdot \frac{\sqrt{3}}{2} = \frac{3}{2} = 1,5.\]

\[Ответ:1,5.\]

\[\boxed{\mathbf{24.}}\]

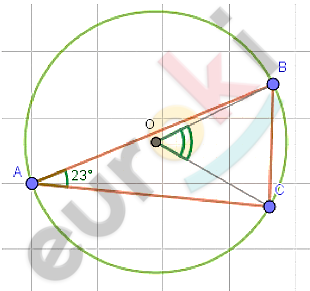
\[⊿ABC;\]

\[(O;R) - описанная\ \]

\[окружность;\]

\[\angle BAC = 23{^\circ}.\]

\[Решение.\]

\[\angle BOC - центральный\ угол\ на\ \]

\[хорде\ BC;\]

\[\angle BAC - вписанный\ угол\ на\ \]

\[хорде\ BC:\]

\[\angle BOC = 2\angle BAC = 2 \cdot 23 = 46{^\circ}.\]

\[Ответ:46{^\circ}.\]

\[\boxed{\mathbf{25.}}\]

\[⊿ABC;AB = BC = 5;AC = 6;\]

\[(O;r) - вписанная\ окружность.\]

\[Решение.\]

\[1)\ Проведем\ BH\bot AC.\]

\[2)\ ⊿ABC - равнобедренный:\]

\[BH - высота,\ медиана\ и\ \]

\[биссектриса.\]

\[3)\ Проведем\ AK - биссектрису:\]

\[O - точка\ пересечения\ \text{BH\ }и\ \]

\[AK;или\ точка\ пересечения\ \]

\[биссектрис;\]

\[O - центр\ вписанной\ \]

\[окружности.\]

\[Отсюда:\]

\[OH\bot AC;H - точка\ касания\ \]

\[окружности\ и\ AC;\]

\[r = OH.\]

\[4)\ r = OH = AH \cdot tg\ \angle OAH =\]

\[= AH \cdot tg\frac{A}{2};\]

\[AH = \frac{\text{AC}}{2} = 3;\]

\[\cos A = \frac{\text{AH}}{\text{AB}} = \frac{3}{5} = 0,6;\]

\[tg^{2}A = \frac{1 - \cos A}{1 + \cos A} = \frac{1 - 0,6}{1 + 0,6} =\]

\[= \frac{0,4}{1,6} = \frac{1}{4};\]

\[tg\ A = \frac{1}{2}.\]

\[5)\ Получаем:\]

\[r = 3 \cdot \frac{1}{2} = 1,5.\]

\[Ответ:1,5.\]

Задание 8

\[\boxed{\mathbf{Задание\ 8.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[a = 3;b = 8;c = 5.\]

\[Квадрат\ диагонали\ \]

\[прямоугольного\ \]

\[параллелепипеда\ равен\]

\[сумме\ квадратов\ его\ \]

\[измерений:\]

\[d^{2} = 3^{2} + 8^{2} + 5^{2} =\]

\[= 9 + 64 + 25 = 98.\]

\[Ответ:98.\]

\[\boxed{\mathbf{2.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[AB = 5;AD = 4;AA_{1} = 4.\]

\[\angle C_{1}BC - лежит\ в\ плоскости\ \]

\[грани\ \text{BC}C_{1}B_{1}:\]

\[BC = AD = 4;\ \ CC_{1} = AA_{1} = 4.\]

\[\text{BC}C_{1}B_{1} - квадрат:\]

\[BC_{1} - диагональ\ и\ биссектриса\ \]

\[прямоуго\ угла:\]

\[\angle C_{1}BC = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{3.}}\]

\[SABC - правильная\ \]

\[треугольная\ пирамида;\]

\[S - вершина;\]

\[R - середина\ ребра\ BC;\]

\[AB = 1;\ \ SR = 2.\]

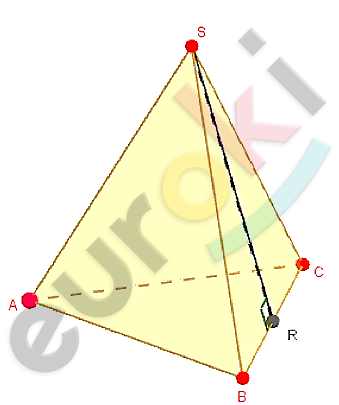
\[S_{бок} = 3S_{⊿}.\]

\[⊿SBC - равнобедренный:\]

\[SR - медиана,\ биссектриса\ и\ \]

\[высота\ боковой\ грани.\]

\[S_{⊿} = \frac{1}{2}BC \cdot SR = \frac{1}{2} \cdot 1 \cdot 2 = 1.\]

\[S_{бок} = 3 \cdot 1 = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{4.}}\]

\[SABC - правильная\ \]

\[треугольная\ пирамида;\]

\[AA_{1};\ \ BB_{1};\ \ \ CC_{1} - медианы;\]

\[M - точка\ пересечения\ \]

\[медиан;\]

\[MS = 1;V = 1.\]

\[M - центр\ правильного\ ⊿ABC;\]

\[S - проецируется\ в\ M;\]

\[MS\bot\left( \text{ABC} \right);\]

\[MS - высота\ пирамиды.\]

\[V = \frac{1}{3} \cdot S_{\text{ABC}} \cdot MS\]

\[S_{\text{ABC}} = \frac{3V}{\text{MS}} = \frac{3 \cdot 1}{1} = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{5.}}\]

\[Дано:\]

\[AC = 6;\]

\[SH\bot\left( \text{ABC} \right) - высота;\]

\[SH = 4.\]

\[Решение.\]

\[Вершина\ S - проецируется\ в\ \]

\[точку\ пересечения\ \]

\[диагоналей\ H:\]

\[AH = \frac{1}{2}AC = 3;\]

\[SA = \sqrt{SH^{2} + AH^{2}} =\]

\[= \sqrt{4^{2} + 3^{2}} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{6.}}\]

\[Дано:\]

\[a = 23.\]

\[Решение.\]

\[DF - малая\ диагональ\ \]

\[шестиугольника;\]

\[\angle E = 120{^\circ}.\]

\[По\ теореме\ косинусов:\]

\[DF^{2} =\]

\[= EF^{2} + ED^{2} - 2EF \cdot ED \cdot \cos{120{^\circ}} =\]

\[= a^{2} + a^{2} - 2a^{2} \cdot \left( - \frac{1}{2} \right) = 3a^{2}.\]

\[По\ теореме\ Пифагора:\]

\[DF_{1}^{2} = DF^{2} + EF_{1}^{2} =\]

\[= 3a^{2} + a^{2} = 4a^{2}\]

\[DF_{1} = \sqrt{4a²} = 2a = 2 \cdot 23 = 46.\]

\[Ответ:46.\]

\[\boxed{\mathbf{7.}}\]

\[Дано:\]

\[a = 49.\]

\[Решение.\]

\[AE - малая\ диагональ\ \]

\[шестиугольника;\]

\[\angle F = 120{^\circ}.\]

\[По\ теореме\ косинусов:\]

\[AE^{2} =\]

\[= AF^{2} + EF^{2} - 2AF \cdot EF \cdot \cos{120{^\circ}} =\]

\[= a^{2} + a^{2} - 2a^{2} \cdot \left( - \frac{1}{2} \right) = 3a^{2};\]

\[AE = a\sqrt{3}.\]

\[tg\angle E_{1}EA_{1} = \frac{\text{AE}}{EE_{1}} = \frac{a\sqrt{3}}{2a} = \sqrt{3};\]

\[\angle E_{1}EA_{1} = 60{^\circ}.\]

\[Ответ:60{^\circ}.\]

\[\boxed{\mathbf{8.}}\]

\[Конус;\]

\[h = 4;\ \ 2r = 6:\]

\[r = 3.\]

\[По\ теореме\ Пифагора\ \]

\[образующая\ конуса\ равна:\]

\[l = \sqrt{r^{2} + h^{2}} = \sqrt{3^{2} + 4^{2}} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{9.}}\]

\[Цилиндр;\]

\[S_{бок} = 2\pi;\ \ 2r = 1.\]

\[r = \frac{1}{2}:\]

\[S_{бок} = 2\pi rh = 2\pi\]

\[2\pi \cdot \frac{1}{2} \cdot h = 2\pi\]

\[h = 2\pi\ :\pi\]

\[h = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{10.}}\]

\[Кубы;\]

\[b = 3a.\]

\[Отношение\ объемов:\]

\[\frac{V_{b}}{V_{a}} = \frac{b^{3}}{a^{3}} = \frac{(3a)^{3}}{a^{3}} = 3^{3} = 27.\]

\[Ответ:27.\]

\[\boxed{\mathbf{11.}}\]

\[Куб;\]

\[g = \sqrt{8} - диагональ\ грани.\]

\[Пусть\ ребро\ куба\ равно\ a:\]

\[g = a\sqrt{2}\]

\[a = \frac{g}{\sqrt{2}} = \frac{\sqrt{8}}{\sqrt{2}} = \sqrt{4} = 2.\]

\[V = a^{3} = 2^{3} = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{12.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[V = 60;\ \ S_{грани} = 12.\]

\[V = S \cdot a;где\ a\bot\left( \text{ABCD} \right):\]

\[a = \frac{V}{S} = \frac{60}{12} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{13.}}\]

\[Прямоугольный\ \]

\[параллелепипед;\]

\[a = 2;\ \ b = 6;\ \ V = 48:\]

\[V = abc\]

\[c = \frac{V}{\text{ab}} = \frac{48}{2 \cdot 6} = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{14.}}\]

\[Прямоугольный\ ⊿ - основание\ \]

\[прямой\ треугольной\ призмы;\]

\(a = 6;\ \ b = 8;\ \ h = 5.\)

\[S_{осн} = \frac{1}{2}a \cdot b;\]

\[V = S_{осн} \cdot h = \frac{1}{2}a \cdot b \cdot h =\]

\[= \frac{1}{2} \cdot 6 \cdot 8 \cdot 5 = 120.\]

\[Ответ:120.\]

\[\boxed{\mathbf{15.}}\]

\[В\ основании\ призмы\ лежит\ \]

\[треугольник,\ средняя\ линия\ \]

\[проходит\ через\ середины\ двух\ \]

\[соседних\ сторон\ треугольника\ \]

\[и\ параллельна\ третьей\ \]

\[стороне.\ Длина\ средней\ линии\ \]

\[в\ 2\ раза\ меньше\ стороны,\ \]

\[которой\ она\ параллельна.\ \]

\[Таким\ образом,\ получаем,\ что\ \]

\[меньший\ треугольник\ \]

\[(основание\ отсеченной\ призмы)\]

\[имеет\ линейные\ размеры\ в\ \]

\[2\ раза\ меньшие,\ чем\ исходный\ \]

\[треугольник.\ \]

\[Следовательно,\ площадь\ \]

\[малого\ треугольника\ в\ 4\ раза\ \]

\[меньше\ площади\ исходного.\ \]

\[Высоты\ исходной\ и\ \]

\[отсеченной\ пирамид\ равны.\ \]

\[Получаем,\ что\ объем\ \]

\[отсеченной\ пирамиды\ \]

\[V_{2} = \frac{1}{4}S_{осн} \cdot \text{h\ \ }меньше\ \]

\[исходного\ объема\ V_{1} =\]

\[= S_{осн} \cdot h\ в\]

\[\frac{V_{2}}{V_{1}} = \frac{1}{4}\]

\[V_{2} = \frac{1}{4}V_{1}.\]

\[V_{1} = 32:\]

\[V_{2} = \frac{32}{4} = 8.\]

\[Ответ:8.\]

\[\boxed{\mathbf{16.}}\]

\[Правильная\ шестиугольная\ \]

\[призма;\]

\[a = 1 - сторона\ основания;\]

\[h = \sqrt{3} - боковое\ ребро.\]

\[Правильный\ шестиугольник\ \]

\[состоит\ из\ 6\ правильных\ \]

\[треугольников:\]

\[S_{1} = \frac{1}{2}a \cdot b \cdot \sin{60{^\circ}} =\]

\[= \frac{1}{2} \cdot 1 \cdot 1 \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{4};\]

\[S_{осн} = 6S_{1} = 6 \cdot \frac{\sqrt{3}}{4} = \frac{3\sqrt{3}}{2}.\]

\[V = S_{осн} \cdot h = \frac{3\sqrt{3}}{2} \cdot \sqrt{3} = \frac{9}{2} =\]

\[= 4,5.\]

\[Ответ:4,5.\]

\[\boxed{\mathbf{17.}}\]

\[Объем\ призмы:\]

\[V = S_{осн} \cdot \text{h.}\]

\[В\ основании\ призмы\ лежит\ \]

\[правильный\ шестиугольник\ \]

\[со\ сторонами\ 2.\ Его\ площадь\ \]

\[равна\ площади\ 6\ \]

\[равносторонним\ \]

\[треугольникам\ со\ сторонами\ 2.\]

\[Площадь\ одного\ треугольника:\]

\[S = \frac{1}{2}ab \cdot \sin{60{^\circ}} =\]

\[= \frac{1}{2} \cdot 2 \cdot 2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3}.\]

\[Площадь\ основания:\]

\[S = 6S = 6\sqrt{3}.\]

\[Высота\ призмы:\]

\[h = 2\sqrt{3} \cdot \sin{30{^\circ}} = 2\sqrt{3} \cdot \frac{1}{2} =\]

\[= \sqrt{3}.\]

\[Объем\ призмы:\]

\[V = 6\sqrt{3} \cdot \sqrt{3} = 6 \cdot 3 = 18.\]

\[Ответ:18.\]

\[\boxed{\mathbf{18.}}\]

\[Дано:\]

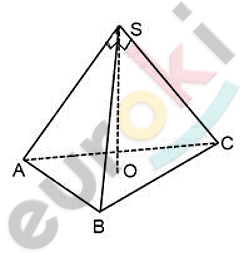
\[боковое\ ребро = 3.\]

\[Решение.\]

\[В\ качестве\ основания\ \]

\[пирамиды\ выберем\ \]

\[треугольник\ ASB.\ \]

\[Тогда\ высотой\ пирамиды\ будет\ \]

\[выступать\ отрезок\ SC.\ \]

\[Площадь\ треугольника\ ASB\ \]

\[(то\ есть\ площадь\ основания):\]

\[S = \frac{1}{2}AS \cdot SB = \frac{1}{2} \cdot 3 \cdot 3 = \frac{9}{2}.\]

\[Объем\ пирамиды:\]

\[V = \frac{1}{3} \cdot S \cdot SC = \frac{1}{3} \cdot \frac{9}{2} \cdot 3 = \frac{9}{2} =\]

\[= 4,5.\]

\[Ответ:4,5.\]

\[\boxed{\mathbf{19.}}\]

\[Дано:\]

\[V = 16.\]

\[Решение.\]

\[V = \frac{1}{3}S_{осн} \cdot h;\]

\[S_{осн} = AD \cdot CD = 3 \cdot 4 = 12;\]

\[h = \frac{3V}{S_{осн}} = \frac{3 \cdot 16}{12} = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{20.}}\]

\[Дано:\]

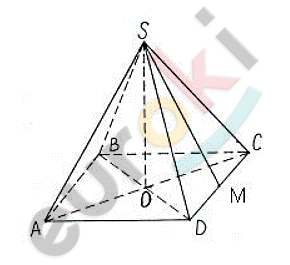
\[h = 12;\]

\[V = 200.\]

\[Решение.\]

\[V = \frac{1}{3}S_{осн} \cdot h\]

\[S_{осн} = \frac{3V}{h} = \frac{3 \cdot 200}{12} = 50.\]

\[Так\ как\ в\ основании\ \]

\[правильной\ четырехугольной\ \]

\[пирамиды\ лежит\ квадрат,\ то\ \]

\[сторона\ квадрата\ будет\ равна:\]

\[a = \sqrt{S_{осн}} = \sqrt{50} = 5\sqrt{2}.\]

\[Вычислим\ диагональ\ по\ \]

\[теореме\ Пифагора:\]

\[d = \sqrt{a^{2} + a^{2}} = \sqrt{50 + 50} = 10.\]

\[Известно,\ что\ высота\ в\ \]

\[правильной\ пирамиде\ делит\ \]

\[диагонали\ пополам.\ \]

\[Следовательно,\ боковую\ грань\ \]

\[можно\ найти\ из\ \]

\[прямоугольного\ треугольника\ \]

\[AOS,\ где\ AO = 5,\ SO = 12:\]

\[AS = \sqrt{AO^{2} + SO^{2}} =\]

\[= \sqrt{25 + 144} = \sqrt{169} = 13.\]

\[Ответ:13.\]

\[\boxed{\mathbf{21.}}\]

\[Дано:\]

\[пирамида\ \text{ABC}C_{1}B_{1};\]

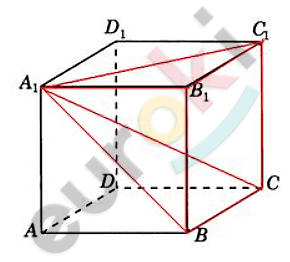
\[AB = 4;AD = 3;AA_{1} = 4.\]

\[Решение.\]

\[BB_{1}C_{1}C - основание\ \]

\[пирамиды:\]

\[V = S_{осн} \cdot \text{h.}\]

\[S_{осн} = BB_{1} \cdot BC;\]

\[h = A_{1}B_{1} = AB:\]

\[V = \frac{1}{3}BB_{1} \cdot BC \cdot AB =\]

\[= \frac{1}{3} \cdot 4 \cdot 3 \cdot 4 = 16.\]

\[Ответ:16.\]

\[\boxed{\mathbf{22.}}\]

\[Дано:\ \]

\[Решение.\]

\[Рассмотрим\ прямоугольный\ \]

\[треугольник\ ASH,\ в\ котором\]

\[высота\ SH = 6,\ угол\ SAH = 60{^\circ},\ \]

\[а\ угол\ ASH = 30{^\circ}.\ \]

\[Тогда\ отрезок\ AH\ будет\ равен:\]

\[tg\angle ASH = \frac{\text{AH}}{\text{SH}}\]

\[AH = SH \cdot tg\ 30{^\circ} = 6 \cdot \frac{\sqrt{3}}{3} =\]

\[= 2\sqrt{3}.\]

\[Треугольник\ ASD\ имеет\ два\ \]

\[угла\ по\ 60{^\circ}.\]

\[Следовательно,\ третий\ \]

\[угол\ ASD\ также\ равен\ 60{^\circ}\ и\ \]

\[треугольник\ ASD - \ \]

\[равносторонний.\ \]

\[В\ равностороннем\ \]

\[треугольнике\ высота\ SH\ делит\ \]

\[основание\ AD\ пополам,\ то\ есть\ \]

\[AD = 2AH\ и\ AD = 4\sqrt{3}.\]

\[Для\ нахождения\ второй\ \]

\[стороны\ основания\ \]

\[рассмотрим\ прямоугольный\ \]

\[треугольник\ SHG,\ в\ котором\ \]

\[угол\ SGH = 60{^\circ}\ по\ условию\ \]

\[задачи.\ \]

\[Следовательно,\ угол\ HSG\ будет\ \]

\[равен\ 30{^\circ}\ \]

\[Аналогично\ находим\ \]

\[длину\ HG:\]

\[HG = SH \cdot tg\ 30{^\circ} = 6 \cdot \frac{\sqrt{3}}{3} =\]

\[= 2\sqrt{3}.\]

\[S_{осн} = AD \cdot HG = 4\sqrt{3} \cdot 2\sqrt{3} =\]

\[= 24.\]

\[V = \frac{1}{3}S_{осн} \cdot h = \frac{1}{3} \cdot 24 \cdot 6 = 48.\]

\[Ответ:48.\]

\[\boxed{\mathbf{23.}}\]

\[Дано:\]

\[S_{пов} = 216.\]

\[Решение.\]

\[Площадь\ поверхности\ куба\ \]

\[равна:\]

\[S = 6a^{2};\ \ a - длина\ грани\ куба.\]

\[a = \sqrt{\frac{S}{6}} = \sqrt{\frac{216}{6}} = \sqrt{36} = 6.\]

\[Сфера\ вписана\ в\ куб,\ поэтому\ \]

\[ее\ радиус\ равен\ половине\ \]

\[длины\ ребра\ куба:\]

\[R = a\ :2 = 6\ :2 = 3.\]

\[Ответ:3.\]

\[\boxed{\mathbf{24.}}\]

\[Объем\ первого\ цилиндра:\]

\[V_{1} = S_{осн} \cdot h = \pi R^{2} \cdot h.\]

\[У\ второго\ цилиндра:\]

\[3h - высота;\]

\[\frac{R}{2} - радиус\ основания.\]

\[Его\ объем:\]

\[V_{2} = \pi \cdot \left( \frac{R}{2} \right)^{2} \cdot 3h = \frac{3}{4}\pi R^{2}\text{h.}\]

\[Получаем,\ что\ он\ в\ \frac{3}{4}\ раза\ \]

\[отличается\ от\ объема\ первого\ \]

\[цилиндра:\]

\[V_{2} = \frac{3}{4} \cdot 12 = 9.\]

\[Ответ:9.\]

\[\boxed{\mathbf{25.}}\]

\[Дано:\]

\[h = BC = 6;\]

\[l = AB = 10.\]

\[Решение.\]

\[\mathrm{\Delta}ABC - прямоугольный.\]

\[По\ теореме\ Пифагора:\]

\[r = AC = \sqrt{BC^{2} - AB^{2}} =\]

\[= \sqrt{100 - 36} = 8.\]

\[S_{осн} = \pi r^{2} = \pi \cdot 64.\]

\[V = \frac{1}{3}BC \cdot S_{осн} = \frac{1}{3} \cdot 6 \cdot 64\pi =\]

\[= 128\pi.\]

\[\frac{V}{\pi} = 128.\]

\[Ответ:128.\]

\[\boxed{\mathbf{26.}}\]

\[Дано:\]

\[d_{осн} = 6.\]

\[Решение.\]

\[Конус,\ у\ которого\ образующие\ \]

\[пересекаются\ под\ прямым\ \]

\[углом,\ вписывается\ в\ шар.\ \]

\[Причем,\ диаметр\ шара\ равен\ \]

\[диаметру\ основания\ конуса,\ а\ \]

\[радиус\ шара\ равен\ высоте\ \]

\[конуса,\ то\ есть\ высота\ конуса\ \]

\[равна:h = d\ :2 = 6\ :2 = 3.\]

\[V = \frac{1}{3}h \cdot S_{осн} = \frac{1}{3}h \cdot \pi \cdot \left( \frac{d}{2} \right)^{2} =\]

\[= \frac{1}{3} \cdot 3 \cdot \frac{36\pi}{4} = 9\pi.\]

\[\frac{V}{\pi} = \frac{9\pi}{\pi} = 9.\]

\[Ответ:9.\]

\[\boxed{\mathbf{27.}}\]

\[k = \frac{b}{a} = 2 - коэффициент\ \]

\[подобия\ кубов.\]

\[\frac{S_{2}}{S_{1}} = k^{2} = 4\ (раза) -\]

\[увеличится\ площадь.\]

\[Ответ:в\ 4\ раза.\]

\[\boxed{\mathbf{28.}}\]

\[k = \frac{b}{a} = \frac{1}{4} - коэффициент\ \]

\[подобия\ тетраэдров.\]

\[\frac{S_{2}}{S_{1}} = k^{2} = \frac{1}{16} - отношение\ \]

\[площадей.\]

\[S_{2} = \frac{1}{16}S_{1} = \frac{80}{16} = 5\ см^{2}.\]

\[Ответ:5\ см^{2}.\]

\[\boxed{\mathbf{29.}}\]

\[S_{1} = \pi r_{1}l_{1};\ \ \ \ S_{2} = \pi r_{2}l_{2}:\]

\[\frac{S_{2}}{S_{1}} = \frac{\pi r_{1}l_{1}}{\pi r_{2}l_{2}} = \frac{\frac{r_{1}}{4} \cdot 2l_{1}}{r_{1}l_{1}} = \frac{1}{2};\]

\[S_{2} = \frac{1}{2}S_{1} = \frac{1}{2} \cdot 16 = 8\ \left( см^{2} \right).\]

\[Ответ:8\ см^{2}.\]

Задание 14

\[\boxed{\mathbf{14.}\ ОК\ ГДЗ - домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[Дано:\]

\[AC_{1} - прямая.\]

\[Решение.\]

\[Проекция\ прямой\ AC_{1}\ на\ \]

\[грань - прямая\ BC_{1}\]

\[\angle AC_{1}B - искомый.\]

\[Пусть\ BC = 1;\ \ \]

\[BC_{1} = \sqrt{2} - как\ диагональ\ \]

\[квадрата.\]

\[⊿\text{BC}C_{1} - прямоугольный:\]

\[tg\angle BCC_{1} = \frac{\sqrt{2}}{2}.\]

\[Ответ:\ \frac{\sqrt{2}}{2}.\]

\[\boxed{\mathbf{2.}}\]

\[Дано:\]

\[Найти:\]

\[\cos{\angle\left( AA_{1};BC_{1}D \right)}.\]

\[Решение.\]

\[1)\ Пусть\ сторона\ куба\ AB = a.\]

\[2)\ CC_{1} \parallel AA_{1}:\]

\[\angle\left( AA_{1}BC_{1}D \right) = \angle\left( CC_{1};BC_{1}D \right).\]

\[3)\ M - середина\ \text{BD.}\]

\[CM\bot BD;\ \ C_{1}M\bot BD - по\ \]

\[признаку\ перпендикулярности\ \]

\[прямой\ и\ плоскости:\]

\[CC_{1}M\bot BD;\]

\[CC_{1}M\bot BC_{1}\text{D.}\]

\[4)\ CH\bot MC_{1};\ \ CC_{1} - наклонная:\]

\[HC_{1} - проекция;\]

\[\angle\left( CC_{1};BC_{1}D \right) = \angle CC_{1}H - угол\ \]

\[между\ прямой\ и\ плоскостью.\]

\[5)\ Пусть\ \angle CC_{1}H = \alpha.\]

\[6)\ В\ треугольнике\ \text{MC}C_{1}:\]

\[\angle MCC_{1} = 90{^\circ};\]

\[CC_{1} = a;\]

\[MC = \frac{\text{AC}}{2} = \frac{a\sqrt{2}}{2}.\]

\[Отсюда:\]

\[tg\ \alpha = \frac{\text{MC}}{CC_{1}} = \frac{a\sqrt{2}}{2a} = \frac{\sqrt{2}}{2}.\]

\[7)\cos\alpha = \frac{1}{\sqrt{1 + tg^{2}\alpha}} =\]

\[= \frac{1}{\sqrt{1 + \left( \frac{\sqrt{2}}{2} \right)^{2}}} = \frac{1}{\sqrt{\frac{3}{2}}} = \sqrt{\frac{2}{3}}.\]

\[Ответ:\ \sqrt{\frac{2}{3}}.\]

\[\boxed{\mathbf{3.}}\]

\[Дано:\]

\[Диагонали\ квадрата\ \]

\[пересекаются\ под\ прямым\ \]

\[углом:\]

\[BA_{1}\bot AB_{1}.\]

\[Тогда:\]

\[B_{1}C_{1}\bot\left( A_{1}\ B_{1}B \right);\]

\[B_{1}C_{1}\bot BA_{1}.\]

\[BA_{1}\bot AB_{1};\ \ BA_{1}\bot B_{1}C_{1}:\]

\[BA_{1}\bot\left( AB_{1}C_{1} \right).\]

\[Аналогично\ получаем:\]

\[BC_{1}\bot\left( A_{1}B_{1}C \right).\]

\[Угол\ между\ плоскостями\ равен\ \]

\[углу\ между\ номрмалями\ к\ ним:\]

\[\angle\left( AB_{1}C_{1};A_{1}B_{1}C \right) = \angle\left( BA_{1};BC_{1} \right).\]

\[⊿BA_{1}C_{1} - равносторонний:\]

\[все\ стороны - диагонали\ куба.\]

\[Значит:\]

\[\angle C_{1}BA_{1} = 60{^\circ}.\]

\[Ответ:60{^\circ}.\]

\[\boxed{\mathbf{4.}}\]

\[Дано:\]

\[AA_{1} = 5;\ \ AB = 12;AD = 8;\]

\[K - середина\ C_{1}D_{1};\]

\[\alpha\bot AK.\]

\[Найти:\]

\[tg\ \angle(ABC;\alpha).\]

\[Решение.\]

\[1)\ Построим\ KK_{1}\bot CD;\]

\[BH\bot AK_{1};\]

\[E - точка\ пересечения\ \]

\[AK_{1}\ и\ \text{BH}.\]

\[2)\ Построим\ EE_{1}\bot AK;\ \ \]

\[P - точка\ пересечения.\]

\[3)\ EE_{1}\bot AK;\ \ AE\bot BH:\]

\[\angle AEE_{1} = \angle(ABC;\alpha) -\]

\[линейный\ угол\ двугранного\ \]

\[угла.\]

\[4)\ Достроим\ сечение\ \]

\[параллелепипеда\ плоскостью\ \]

\[\alpha:проведем\ NM \parallel BH\ и\ \ \]

\[HG \parallel BN.\]

\[5)\ В\ треугольнике\ \text{AD}K_{1}:\]

\[\angle ADK_{1} = 90{^\circ};\]

\[AD = 8;\]

\[DK_{1} = \frac{\text{AB}}{2} = 6.\]

\[Отсюда:\]

\[AK_{1} = \sqrt{AD^{2} + DK_{1}^{2}} =\]

\[= \sqrt{8^{2} + 6^{2}} = 10.\]

\[6)\ В\ треугольнике\ \text{AK}K_{1}:\]

\[\angle AK_{1}K = 90{^\circ};\]

\[AK_{1} = 10;\]

\[KK_{1} = AA_{1} = 5.\]

\[Отсюда:\]

\[tg\ \angle KAK_{1} = \frac{KK_{1}}{AK_{1}} = \frac{5}{10} = \frac{1}{2}.\]

\[7)\ В\ треугольнике\ APE:\]

\[\angle APE = 90{^\circ};\]

\[\angle AEP = 90{^\circ} - \angle KAK_{1}.\]

\[Отсюда:\]

\[tg\ \angle AEP = tg\ \left( 90{^\circ} - \angle KAK_{1} \right) =\]

\[= ctg\ \angle KAK_{1} = 1\ :\frac{1}{2} = 2.\]

\[tg\ \angle AEE_{1} = tg\ \angle AEP = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{5.}}\]

\[Дано:\]

\[\text{ABC}A_{1}B_{1}C_{1} - прямая\ призма;\]

\[⊿ABC - основание;AC -\]

\[гипотенуза;\]

\[AB = 4;\]

\[BB_{1} = 12.\]

\[Найти:\]

\[tg\ \angle\left( A_{1}B_{1}C_{1};\alpha \right).\]

\[Решение.\]

\[1)\ BB_{1}\bot ABC:\]

\[\text{AB}B_{1}\bot ABC.\]

\[2)\ Продолжим\ прямые\ A_{1}B_{1}\ и\ \]

\[\text{BM},\ лежащие\ в\ одной\ \]

\[плоскости:\]

\[D - точка\ их\ пересечения.\]

\[Проведем\ DE \parallel BC.\]

\[3)\ BC\bot ABB_{1}:\]

\[DE\bot ABB_{1};\ \ DE\bot A_{1}B_{1};\ \ \]

\[DE\bot BM.\]

\[Отсюда:\]

\[DE - ребро\ двугранного\ угла;\]

\[\angle BDB_{1} = \angle\left( A_{1}B_{1}C_{1};\alpha \right) -\]

\[линейный\ угол\ двугранного\ \]

\[угла.\]

\[4)\ AM - средняя\ линия\ ⊿DBB_{1}:\]

\[AM \parallel B_{1}B;\ \ \ AM = \frac{1}{2}B_{1}\text{B.}\]

\[Отсюда:\]

\[DA_{1} = A_{1}B_{1} = AB = 4.\]

\[5)\ В\ треугольнике\ \text{DB}B_{1}:\]

\[\angle DB_{1}B = 90{^\circ};\]

\[DB_{1} = DA_{1} + A_{1}B_{1} = 8;\]

\[BB_{1} = 12.\]

\[Отсюда:\]

\[tg\angle BDB_{1} = \frac{BB_{1}}{DB_{1}} = \frac{12}{8} = 1,5.\]

\[Ответ:1,5.\]

\[\boxed{\mathbf{6.}}\]

\[Дано:\]

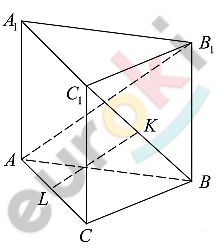
\[Решение.\]

\[1)\ CC_{1} = C_{1}B = B_{1}B = BC;\ \ \]

\[\text{ABC}A_{1}B_{1}C_{1} - правильная\ \]

\[призма:\]

\[CC_{1}B_{1}B - квадрат.\]

\[2)\ Отсюда:\]

\[K - точка\ пересечения\ \]

\[диагоналей\ квадрата,\ так\ как\ \]

\[делит\ одну\ из\ них\ пополам.\]

\[3)\ Значит:\]

\[B_{1}K = KC.\]

\[Тогда\ KL - средняя\ линия\ \]

\[треугольника\ AB_{1}C:\]

\[KL \parallel AB_{1}.\]

\[4)\ Необходимо\ найти\ угол\ \text{LKB.}\]

\[По\ теореме\ Пифагора:\]

\[AB_{1} = C_{1}B = \sqrt{2};\]

\[BK = KL = \frac{\sqrt{2}}{2}.\]

\[LB = \frac{\sqrt{3}}{2} - высота\ правильного\ \]

\[⊿\text{ABC.}\]

\[По\ теореме\ косинусов:\]

\[LB^{2} =\]

\[= KL^{2} + BK^{2} - 2KL \cdot BK \cdot \cos{\angle LKB}\]

\[2 \cdot \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} \cdot \cos{\angle LKB} =\]

\[= \left( \frac{\sqrt{2}}{2} \right)^{2} + \left( \frac{\sqrt{2}}{2} \right)^{2} - \left( \frac{\sqrt{3}}{2} \right)^{2}\]

\[\cos{\angle LKB} = \frac{2}{4} + \frac{2}{4} - \frac{3}{4}\]

\[\cos{\angle LKB} = \frac{1}{4} = 0,25.\]

\[Ответ:0,25.\]

\[\boxed{\mathbf{7.}}\]

\[Дано:\]

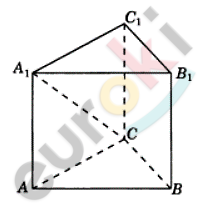
\[Решение.\]

\[Прямые\ AB\ и\ A_{1}C -\]

\[скрещивающиеся.\ Нам\ нужно\ \]

\[найти\ угол\ между\ этими\ двумя\ \]

\[скрещивающимися\ прямыми.\]

\[Отмечаем\ на\ кубе\ отрезок\ A_{1}B_{1},\]

\[параллельный\ отрезку\ AB/\]

\[Прямые\ A_{1}B_{1}и\ A_{1}C -\]

\[пересекающиеся,\ наименьшим\ \]

\[углом\ между\ ними\ является\ \]

\[угол\ CA_{1}B_{1}.\]

\[Так\ как\ прямая\ A_{1}B_{1} \parallel отрезку\ \]

\[AB;\ \ \angle CA_{1}B_{1} - \ является\ \]

\[искомым\ углом\ между\ \]

\[прямыми\ AB\ и\ A_{1}\text{C.}\]

\[По\ свойствам\ правильной\ \]

\[треугольной\ призмы:\]

\[A_{1}C = B_{1}C = \sqrt{2} \cdot 1 = \sqrt{2}.\]

\[По\ теореме\ косинусов\ \]

\[\left( из\ ⊿A_{1}B_{1}C \right):\]

\[Подставим:\]

\[\left( \sqrt{2} \right)^{2} =\]

\[= 1^{2} + \left( \sqrt{2} \right)^{2} - 2 \cdot 1 \cdot \sqrt{2} \cdot \cos{CA_{1}B_{1}}\]

\[2 = 3 - 2\sqrt{2}\cos{CA_{1}B_{1}}\]

\[\cos{CA_{1}B_{1}} = \frac{1}{2\sqrt{2}}.\]

\[Ответ:\ \frac{1}{2\sqrt{2}}.\]

\[\boxed{\mathbf{8.}}\]

\[Дано:\]

\[\text{ABC}A_{1}B_{1}C_{1} - правильная\ \]

\[призма;\]

\[ребра\ равны\ 1;\]

\[ABC;CA_{1}B_{1} - плоскости.\]

\[Найти:\]

\[tg\ \angle\left( ABC;CA_{1}B_{1} \right).\]

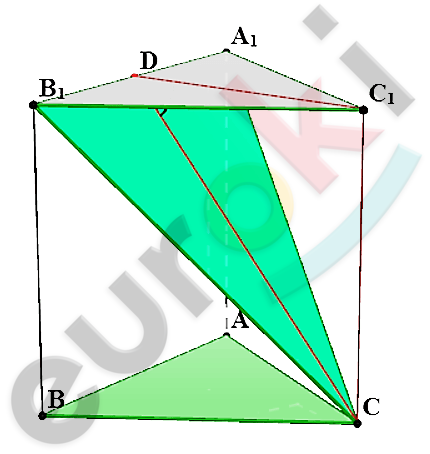
\[Решение.\ \]

\[1)\ \left( A_{1}B_{1}C_{1} \right) \parallel \left( \text{ABC} \right):\]

\[\angle\left( A_{1}B_{1}C_{1};A_{1}B_{1}C \right) =\]

\[= \angle\left( ABC;A_{1}B_{1}C \right).\]

\[2)\ Построим\ плоскость\ \]

\[\text{CD}C_{1}\bot A_{1}B_{1}.\]

\[3)\ A_{1}B_{1}C\ и\ \text{CD}C_{1}\ пересекаются\ \]

\[по\ прямой\ CD;\]

\[A_{1}B_{1}C_{1}\ и\ \text{CD}C_{1}\ пересекаются\ по\ \]

\[прямой\ DC_{1}.\]

\[4)\ По\ определению:\]

\[\angle\left( A_{1}B_{1}C_{1};A_{1}B_{1}C \right) = \angle CDC_{1}\text{.\ }\]

\[5)\ По\ свойствам\ правильной\ \]

\[треугольной\ призмы:\]

\[C_{1}D = \frac{\sqrt{3}}{2} \cdot 1;\]

\[CC_{1} = 1;\]

\[\angle CC_{1}D = 90{^\circ}.\]

\[6)\ ⊿\text{CD}C_{1} - прямоугольный:\]

\[tg\ \angle CDC_{1} = \frac{CC_{1}}{C_{1}D} = 1\ :\frac{\sqrt{3}}{2} = \frac{2}{\sqrt{3}}.\]

\[Ответ:\ \frac{2}{\sqrt{3}}.\]

\[\boxed{\mathbf{9.}}\]

\[Дано:\]

\[AC = BC = AB = 2;\]

\[A_{1}B = \sqrt{5}.\]

\[Решение.\ \]

\[H - середина\ ребра\ \text{BC.}\]

\[⊿ABC - равносторонний;\ \]

\[⊿A_{1}BC - равнобедренный;\]

\[AH\bot BC;\ \ AH_{1}\bot BC:\]

\[\angle A_{1}HA - линейный\ угол\ \]

\[двугранного\ угла\ с\ гранями\ \]

\[\text{BCA\ }и\ \text{BC}A_{1}.\]

\[В\ треугольнике\ A_{1}AB:\]

\[AA_{1} = \sqrt{A_{1}B^{2} - AB^{2}} = \sqrt{5 - 4} =\]

\[= 1.\]

\[В\ треугольнике\ AHB:\]

\[AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{4 - 1} =\]

\[= \sqrt{3}.\]

\[В\ треугольнике\ HAA_{1}:\]

\[tg\ \angle A_{1}HA = \frac{AA_{1}}{\text{AH}} = \frac{1}{\sqrt{3}};\]

\[\angle A_{1}HA = 30{^\circ} - искомый.\]

\[Ответ:30{^\circ}.\]

\[\boxed{\mathbf{10.}}\]

\[Дано:\]

\[AB = BC = 10;\]

\[AC = 16;\]

\[BB_{1} = 24;\]

\[P - середина\ BB_{1}.\]

\[Найти:\]

\[tg\ \angle\left( A_{1}B_{1}C_{1};ACP \right).\]

\[Решение.\]

\[Основания\ призмы\ всегда\ \]

\[параллельны,\ поэтому\ тангенс\ \]

\[угла\ между\ плоскостями\ \]

\[\left( A_{1}B_{1}C_{1} \right)и\ \left( \text{ACP} \right),\ который\ \]

\[нужно\ найти,\ равен\ тангенсу\ \]

\[угла\ между\ плоскостями\ \left( \text{ABC} \right)\]

\[и\ (ACP),\ который\ будем\ искать.\]

\[\angle(ABC;ACP) = \angle BQP;\ \ \]

\[BQ - высота\ ⊿ABC.\]

\[⊿ABC - равнобедренный:\]

\[BQ - еще\ и\ медиана;\]

\[AQ = \frac{\text{AC}}{2} = \frac{16}{2} = 8.\]

\[По\ теореме\ Пифагора:\]

\[BQ = \sqrt{AB^{2} - AQ^{2}} =\]

\[= \sqrt{10^{2} - 8^{2}} = 6.\]

\[BP = \frac{BB_{1}}{2} = \frac{24}{2} = 12:\]

\[tg\ \angle BQP = \frac{\text{BP}}{\text{BQ}} = \frac{12}{6} = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{11.}}\]

\[Дано:\]

\[Решение.\]

\[Призма\ прямая,\ в\ основании\ \]

\[прямоугольник.\ \]

\[Значит,\ она\ еще\ и\ \]

\[прямоугольный\ \]

\[параллелепипед.\]

\[Это\ значит,\ что\ расстояние\ \]

\[между\ A_{1}C_{1}\ и\ BD\ \]

\[(диагоналями\ оснований\ призмы)\]

\[равно\ длине\ боковых\ \]

\[ребер - \sqrt{3}\text{.\ }\]

\[Нам\ нужно\ найти\ тангенс\ угла\ \]

\[между\ боковой\ гранью\ AA_{1}D_{1}\text{D\ }\]

\[и\ плоскостью,\ \]

\[перпендикулярной\ диагонали\]

\[B_{1}D\ параллелепипеда.\ \]

\[Имеем\ две\ пересекающиеся\ \]

\[плоскости,\ к\ одной\ из\ которых\ \]

\[проведена\ перпендикулярная\ \]

\[прямая\ B_{1}D,\ пересекающая\ \]

\[другую\ плоскость\ в\ точке\ D.\]

\[По\ сути,\ нам\ надо\ найти\ угол\ \]

\[между\ плоскостью\ грани\ \]

\[AA_{1}D_{1}D\ и\ самой\ диагональю\ \]

\[B_{1}D\ - \ угол\ \varphi,\ а\ искомый\ угол\ \]

\[будет\ равен\ (90{^\circ}\ - \ \varphi).\]

\[Поскольку\ мы\ имеем\ дело\ с\ \]

\[прямоугольным\ \]

\[параллелепипедом,\ то\ этот\ \]

\[угол\ легко\ найти\ из\ \]

\[прямоугольного\ \mathrm{\Delta}B_{1}DA_{1}\text{.\ }\]

\[По\ теореме\ Пифагора\ \]

\[\left( из\ ⊿AA_{1}D \right):\]

\[A_{1}D = \sqrt{\left( \sqrt{33} \right)^{2} + \left( \sqrt{3} \right)^{2}\ } =\]

\[= \sqrt{36} = 6.\]

\[Угол\ \varphi\ - \ и\ есть\ угол\ между\ \]

\[гранью\ и\ диагональю.\]

\[ctg\ \varphi = \frac{6}{5};\]

\[\text{tg\ }(90{^\circ} - \varphi) = ctg\ \varphi = \frac{6}{5}.\]

\[Ответ:\frac{6}{5}.\]

\[\boxed{\mathbf{12.}}\]

\[Дано:\]

\[все\ ребра\ равны\ 1.\]

\[Найти:\]

\[tg\ \angle\left( ABC;DB_{1}F_{1} \right).\]

\[Решение.\]

\[Отметим\ точку\ K - середину\]

\[B_{1}F_{1}.\]

\[K \in A_{1}D_{1}:\]

\[D_{1}K\bot B_{1}F_{1}.\]

\[B_{1}F_{1}\bot AA_{1}D_{1}:\]

\[DK\bot B_{1}F_{1}.\]

\[Тогда:\]

\[tg\angle\left( ABC;DB_{1}F_{1} \right) =\]

\[= tg\ \angle\left( A_{1}B_{1}C_{1};DB_{1}F_{1} \right) =\]

\[= tg\ \angle D_{1}KD = \frac{D_{1}D}{D_{1K}} =\]

\[= \frac{1}{\frac{3}{4}D_{1}A_{1}} = \frac{2}{3}.\]

\[Ответ:\frac{2}{3}.\]

\[\boxed{\mathbf{13.}}\]

\[Дано:\]

\[Решение.\]

\[AA_{1}\bot DE;\ \ AE\bot DE:\]

\[Плоскость\ \text{DE}A_{1},\ содержащая\ \]

\[прямую\ DE,\bot плоскости\ \text{AE}A_{1}.\]

\[Значит,\ искомое\ расстояние\ \]

\[равно\ высоте\ AH\ \]

\[прямоугольного\ ⊿AEA_{1}:\]

\[AA_{1} = 1;\ \ AE = \sqrt{3};\ \ B_{1}F = 2.\]

\[Отсюда:\]

\[AH = \frac{AA_{1} \cdot AE}{EA_{1}} = \frac{1 \cdot \sqrt{3}}{2} = \frac{\sqrt{3}}{2}.\]

\[Ответ:\ \frac{\sqrt{3}}{2}.\]

\[\boxed{\mathbf{14.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ рёбра\ тетраэдра\ равны\ a,‍\ \]

\[M\ —‍\ проекция\ точки\ E‍\ на\ \]

\[плоскость\ основания\ ABC,‍\ O\ —‍\ \]

\[центр\ равностороннего\ \]

\[треугольника\ ABC.‍\ \]

\[Тогда\ M\ —‍\ середина\ отрезка\ \]

\[OB,‍\ а\ так\ как\ AM\ —‍\ \]

\[ортогональная\ проекция\ \]

\[наклонной\ AE‍\ на\ плоскость\ \]

\[ABC,‍\ то\ угол\ \alpha ‍\ между\ прямой\ \]

\[AE‍\ и\ плоскостью\ ABC\ —‍\ это\ \]

\[угол\ MAE.‍\]

\[В\ прямоугольном\ \]

\[треугольнике\ AOD‍:\]

\[AO = \frac{2}{3} \cdot \frac{a\sqrt{3}}{3} = \frac{a\sqrt{3}}{3};\]

\[DO = \sqrt{AD^{2} - AO^{2}} =\]

\[= \sqrt{a^{2} - \frac{a^{2}}{3}} = a\sqrt{\frac{2}{3}}.\]

\[EM\ —‍\ средняя\ линия\ \]

\[треугольника\ BOD:\]

\[EM = \frac{1}{2}DO = \frac{1}{2}\sqrt{\frac{2}{3}}.\]

\[\sin\alpha = \sin{\angle MAE} = \frac{\text{EM}}{\text{AE}} =\]

\[= \frac{\frac{1}{2} \cdot \sqrt{\frac{2}{3}}}{\frac{a\sqrt{3}}{2}} = \frac{\sqrt{2}}{3}.\]

\[Ответ:\frac{\sqrt{2}}{3}.\]

\[\boxed{\mathbf{15.}}\]

\[Дано:\]

\[Решение.\ \]

\[Вершина\ \text{S\ }проецируется\ в\ \]

\[точку\ H - центр\ правильного\ \]

\[⊿ABC:\]

\[AH = \frac{2}{3}AM = \frac{2}{3} \cdot 6 = 4.\]

\[Угол\ между\ прямой\ и\ \]

\[плоскостью - это\ угол\ между\ \]

\[прямой\ и\ ее\ проекцией\ на\ эту\ \]

\[плоскость:\]

\[\angle(SA;ABC) = \angle SAH.\]

\[В\ треугольнике\ ASH:\]

\[\angle SHA = 90{^\circ};\]

\[SH = 20;\]

\[AH = 4.\]

\[Отсюда:\]

\[tg\ \angle SAH = \frac{\text{SH}}{\text{AH}} = \frac{20}{4} = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{16.}}\]

\[Дано:\]

\[Решение.\]

\[Плоскость\ BED\bot AC\ \]

\[Она\ пересекается\ с\ плоскостью\ \]

\[\text{ACD\ }по\ прямой\ DE;\]

\[с\ плоскостью\ ABC - по\ прямой\ \]

\[\text{EB.}\]

\[Искомый\ угол:\]

\[\angle BED\ между\ прямыми\ \text{ED\ }и\ \text{EB.}\]

\[E - середина\ ребра\ AC:\]

\[AE = \frac{\text{AC}}{2} = 12.\]

\[⊿AEB - прямоугольный:\]

\[BE = \sqrt{AB^{2} - AE^{2}} =\]

\[= \sqrt{13^{2} - 12^{2}} = 5.\]

\[⊿BED - прямоугольный:\]

\[tg\ \angle BED = \frac{\text{BD}}{\text{BE}} = \frac{20}{5} = 4.\]

\[Ответ:4.\]

\[\boxed{\mathbf{17.}}\]

\[Дано:\]

\[Решение.\]

\[Искомое\ расстояние\ от\ \]

\[вершины\ A\ до\ плоскости,\ \]

\[проходящей\ через\ середины\ \]

\[ребер\ AB,\ АС\ и\ AD\ это\ высота\ в\ \]

\[треугольнике\ AKN.\ \]

\[Так\ как\ KN\ и\ AN\ \]

\[перпендикулярны\ ML,\ то\ AH\ \]

\[перпендикуляр.\]

\[По\ теореме\ Пифагора:\]

\[KM = \sqrt{AK^{2} + AM^{2}} =\]

\[= \sqrt{\left( \frac{2\sqrt{5}}{2} \right)^{2} + \left( \frac{10}{2} \right)^{2}} = \sqrt{30}.\]

\[Средняя\ линия:\]

\[ML = \frac{\text{BC}}{2} = 2\sqrt{5}.\]

\[По\ теореме\ Пифагора:\]

\[KN = \sqrt{KM^{2} - MN^{2}} =\]

\[= \sqrt{\left( \sqrt{30} \right)^{2} - \left( \frac{2\sqrt{5}}{2} \right)^{2}} = 5;\]

\[AN = \sqrt{AM^{2} - MN^{2}} =\]

\[= \sqrt{\left( \frac{10}{2} \right)^{2} - \left( \frac{2\sqrt{5}}{2} \right)^{2}} = 2\sqrt{5}.\]

\[Высота\ прямоугольного\ \]

\[треугольника:\]

\[AH = \frac{AK \cdot AN}{\text{KN}} = \frac{\sqrt{5} \cdot 2\sqrt{5}}{5} = 2.\]

\[Ответ:2.\]

\[\boxed{\mathbf{18.}}\]

\[Дано:\]

\[Решение.\ \]

\[1)\ ⊿BDC = ⊿BAC -\]

\[равнобедренные.\]

\[2)\ M - середина\ BC:\]

\[DM - высота\ и\ медиана\ ⊿BDC;\]

\[DM\bot BC.\]

\[AM - высота\ и\ медиана\ ⊿BAC;\]

\[AM\bot BC.\]

\[3)\ По\ признаку\ \]

\[перпендикулярности\ прямой\ и\ \]

\[плоскости:BC\bot ADM.\]

\[4)\ Треугольник\ AMD\ \]

\[равнобедренный,\ и\ его\ медиана\ \]

\[MK,\ проведённая\ к\ AD,\ тоже\ \]

\[является\ высотой.\]

\[Итак,\ MK\ \bot\ AD.\ Кроме\ того,\]

\[MK\ \bot BC\ по\ определению\ \]

\[перпендикулярности\ прямой\ и\ \]

\[плоскости\ (т.к.\ BC\ \bot AMD).\]

\[Это\ значит,\ что\ MK\ и\ есть\ \]

\[общий\ перпендикуляр\ к\ рёбрам\ \]

\[DA\ и\ BC.\]

\[5)\ Найдём\ теперь\ длину\ \]

\[отрезка\ MK:она\ и\ будет\ \]

\[искомым\ расстоянием\ между\ \]

\[прямыми.\]

\[Из\ прямоугольного\ ⊿ABM:\]

\[AM = \sqrt{AB^{2} - BM^{2}} =\]

\[= \sqrt{10^{2} - 6^{2}} = 8.\]

\[Из\ прямоугольного\ ⊿AKM:\]

\[KM = \sqrt{AM^{2} - AK^{2}} =\]

\[= \sqrt{8^{2} - 6^{2}} = \sqrt{28} = 2\sqrt{7}.\]

\[Ответ:2\sqrt{7}.\]

\[\boxed{\mathbf{19.}}\]

\[Дано:\]

\[Решение.\ \]

\[ABCD - квадрат:\]

\[AB\bot AD.\]

\[AB - проекция\ на\ плоскость\ \]

\[SAD:\]

\[AB\bot AD.\]

\[Искомый\ угол\ SMO -\]

\[двугранный\ угол\ при\ ребре\ \]

\[основания\ AD.\]

\[SM - высота\ боковой\ грани\ \]

\[SAD:\]

\[SM = \frac{\sqrt{3}}{2};\ \ MO \parallel AB;\]

\[MO = \frac{1}{2}AB = 0,5.\]

\[В\ прямоугольном\ треугольнике\ \]

\[SMO:\]

\[\cos{\angle SMO} = \frac{\text{MO}}{\text{SM}} = \frac{0,5}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} =\]

\[= \frac{\sqrt{3}}{3}.\]

\[Ответ:\ \frac{\sqrt{3}}{3}.\]

\[\boxed{\mathbf{20.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ AE \parallel BD:\]

\[\angle SBD - искомый.\]

\[2)\ ⊿BDC - равнобедренный:\]

\[KC - медиана,\ высота\ и\ \]

\[биссектриса.\]

\[3)\ ⊿BKC - прямоугольный:\]

\[KC = \frac{1}{2}BC = \frac{1}{2} - как\ катет,\ \]

\[лежащий\ против\ угла\ в\ 30{^\circ}.\]

\[По\ теореме\ Пифагора:\]

\[BK = \sqrt{1^{2} - \left( \frac{1}{2} \right)^{2}} = \sqrt{1 - \frac{1}{4}} =\]

\[= \frac{\sqrt{3}}{2}.\]

\[4)\ BD = 2BK = \frac{2\sqrt{3}}{2} = \sqrt{3};\]

\[BM = \frac{\sqrt{3}}{2};\]

\[\cos{\angle SBM} = \frac{\sqrt{3}}{2}\ :\frac{2}{1} = \frac{\sqrt{3}}{2} \cdot \frac{1}{2} =\]

\[= \frac{\sqrt{3}}{4}.\]

\[Ответ:\frac{\sqrt{3}}{4}.\]

\[\boxed{\mathbf{21.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ Построим\ MN \parallel AC\ и\ \]

\[проходящую\ через\ центр\ \text{O\ }\]

\[основания\ пирамиды.\]

\[2)\ Построим\ \text{SO\ }и\ \text{SM.}\]

\[SM - проекция\ прямой\ \text{MN\ }на\ \]

\[плоскость\ \text{SAF.}\]

\[3)\ По\ определению:\]

\[углом\ между\ прямой\ \text{AC\ }и\ \]

\[плоскость\ \text{SAF\ }будет\ угол\ \text{SMO\ }\]

\[между\ прямой\ \text{MN}\ и\ ее\ \]

\[проекцией\ \text{SM}.\]

\[4)\ NK\bot SM:\]

\[MK - проекция\ MN\ на\ \]

\[плоскость\ SAF.\]

\[5)\ OM = \frac{\sqrt{3}}{2};\]

\[SM^{2} = SA^{2} - AM^{2} =\]

\[= 2^{2} - \left( \frac{1}{2} \right)^{2} = 4 - \frac{1}{4} = \frac{15}{4}\]

\[SM = \frac{\sqrt{15}}{2}.\]

\[\cos{\angle SMO} = \frac{\text{OM}}{\text{SM}} = \frac{\sqrt{3}}{2}\ :\frac{\sqrt{15}}{2} =\]

\[= \frac{\sqrt{3}}{2} \cdot \frac{2}{\sqrt{15}} = \frac{1}{\sqrt{5}}.\]

\[Ответ:\ \frac{1}{\sqrt{5}}.\]

\[\boxed{\mathbf{22.}}\]

\[Первый\ случай:когда\ хорды\ \]

\[находятся\ по\ разные\ стороны\ \]

\[от\ центров\ кругов\ оснований.\]

\[Найдем\ тангенс\ угла\ между\ \]

\[построенной\ плоскостью\ и\ \]

\[плоскостью\ основания\ \]

\[цилиндра.\]

\[В\ треугольнике\ MN_{1}N:\]

\[\angle N = 90{^\circ};\]

\[NN_{1} = OO_{1} = 28.\]

\[В\ треугольнике\ OND:\]

\[\angle N = 90{^\circ};\]

\[ND = 6;\]

\[OD = 10.\]

\[Отсюда:\]

\[ON = \sqrt{OD^{2} - ND^{2}} =\]

\[= \sqrt{100 - 36} = 8.\]

\[В\ треугольнике\ OMB:\]

\[\angle M = 90{^\circ};\]

\[MB = 8;\ \ OB = 10.\]

\[Отсюда:\]

\[OM = \sqrt{OB^{2} - MB^{2}} =\]

\[= \sqrt{100 - 64} = 6.\]

\[MN = OM + ON = 6 + 8 = 14.\]

\[Получаем:\]

\[tg\angle N_{1}MN = \frac{N_{1}N}{\text{MN}} = \frac{28}{14} = 2.\]

\[Второй\ случай:когда\ хорды\ \]

\[находятся\ по\ одну\ сторону\ от\ \]

\[центров\ кругов\ оснований.\]

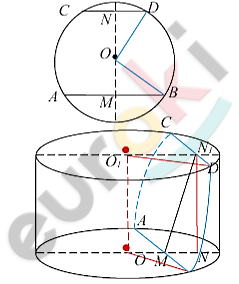
\[В\ треугольнике\ MN_{1}N:\]

\[\angle N = 90{^\circ};\]

\[NN_{1} = OO_{1} = 28.\]

\[В\ треугольнике\ OND:\]

\[\angle N = 90{^\circ};\]

\[ND = 6;\]

\[OD = 10.\]

\[Отсюда:\]

\[ON = \sqrt{OD^{2} - ND^{2}} =\]

\[= \sqrt{100 - 36} = 8.\]

\[В\ треугольнике\ OMB:\]

\[\angle M = 90{^\circ};\]

\[MB = 8;\ \ OB = 10.\]

\[Отсюда:\]

\[OM = \sqrt{OB^{2} - MB^{2}} =\]

\[= \sqrt{100 - 64} = 6.\]

\[MN = ON - OM = 8 - 6 = 2.\]

\[Получаем:\]

\[tg\angle N_{1}MN = \frac{N_{1}N}{\text{MN}} = \frac{28}{2} = 14.\]

\[Ответ:2\ или\ 14.\]

Задание 16

\[\boxed{\mathbf{Задание\ 16.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\boxed{\mathbf{1.}}\]

\[Решение.\]

\[1)\ Поскольку\ медиана\ \]

\[прямоугольного\ треугольника,\ \]

\[проведённая\ из\ вершины\ \]

\[прямого\ угла,\ равна\ половине\ \]

\[гипотенузы:CK = \frac{c}{2}.\]

\[2)\ M - середина\ BC:\]

\[CM = \frac{1}{2}BC = \frac{1}{2}AB \cdot \sin\alpha =\]

\[= \frac{1}{2}c \cdot \sin\text{α.}\]

\[3)\ По\ теореме\ Пифагора\ \]

\[(из\ ⊿ACM):\]

\[AM = \sqrt{AC^{2} + CM^{2}} =\]

\[= \frac{1}{2}c\sqrt{4cos^{2}\alpha + sin^{2}\alpha} =\]

\[= \frac{1}{2}c\sqrt{4cos^{2}\alpha + 1 - cos^{2}\alpha} =\]

\[= \frac{1}{2}c\sqrt{1 + 3cos^{2}\alpha}.\]

\[4)\ Аналогично\ находим\ \]

\[медиану\ BN:\]

\[BN = \frac{1}{2}c\sqrt{1 + 3sin^{2}\alpha}.\]

\[Ответ:\ \frac{1}{2}c\sqrt{1 + 3cos^{2}\alpha};\ \ \]

\[\frac{1}{2}c\sqrt{1 + 3sin^{2}\alpha}.\]

\[\boxed{\mathbf{2.}}\]

\[Дано:\ \]

\[Решение.\]

\[Пусть\ M\ –\ точка\ пересечения\ \]

\[AD\ и\ BE.\ \]

\[Через\ точку\ B\ проведём\ \]

\[прямую,\ параллельную\ \]

\[основанию\ AC,\ и\ продолжим\ \]

\[AD\ до\ пересечения\ с\ этой\ \]

\[прямой\ в\ точке\ T.\ \]

\[Пусть\ \ AE\ = \ a;\ \ AC\ = \ 2a.\]

\[Из\ подобия\ треугольников\ \]

\[BDT\ и\ CDA\ находим:\]

\[BT = \frac{1}{4};\ \ AC = \frac{a}{2}.\]

\[Из\ подобия\ треугольников\ \]

\[AME\ и\ TMB\ находим:\]

\[BM\ :ME = BT\ :AE = 1\ :2.\]

\[Ответ:1\ :2.\]

\[\boxed{\mathbf{3.}}\]

\[Дано:\]

\[AB = BC = 20;\]

\[AC = 5;\]

\[AD - биссектриса.\]

\[Найти:\]

\[\text{AD.}\]

\[Решение.\]

\[Пусть\ CD = x;\ \ \angle A = \angle C = \alpha.\]

\[По\ свойству\ биссектрисы:\]

\[\frac{\text{AB}}{\text{AC}} = \frac{\text{BD}}{\text{CD}}\]

\[\frac{20}{5} = \frac{20 - x}{x}\]

\[20x = 100 - 5x\]

\[25x = 100\]

\[x = 4 - CD.\]

\[E - середина\ \text{AC.}\]

\[В\ треугольнике\ BCE:\]

\[\cos\alpha = \frac{\text{EC}}{\text{BC}} = \frac{5\ :2}{20} = \frac{1}{8}.\]

\[По\ теореме\ синусов\ (⊿ADC):\]

\[\frac{\text{CD}}{\sin\frac{\alpha}{2}} = \frac{\text{AD}}{\sin\alpha}\]

\[AD = \frac{\sin\alpha}{\sin\frac{\alpha}{2}} \cdot CD =\]

\[= \frac{2\sin\frac{\alpha}{2} \cdot \cos\frac{\alpha}{2}}{\sin\frac{\alpha}{2}} \cdot 4 = 8 \cdot \cos\frac{\alpha}{2};\]

\[\cos\frac{\alpha}{2} = \sqrt{\frac{1 + \cos\alpha}{2}} = \sqrt{\frac{1 + \frac{1}{8}}{2}} =\]

\[= \sqrt{\frac{9}{16}} = \frac{3}{4};\]

\[AD = 8 \cdot \frac{3}{4} = 6.\]

\[Ответ:6.\]

\[\boxed{\mathbf{4.}}\]

\[Дано:\]

\[AD - биссектриса;\]

\[AB = 3;\]

\[AC = 6;\]

\[\angle A = 60{^\circ}.\]

\[Найти:\]

\[\text{AD.}\]

\[Решение.\]

\[1)\ E - середина\ отрезка\ \text{AC.}\]

\[2)\ ⊿ABE - равносторонний:\]

\[AB = AE = 3;\]

\[\angle A = 60{^\circ}.\]

\[Отсюда:\]

\[BE = 3.\]

\[3)\ В\ треугольнике\ BEC:\]

\[BE = EC = 3;\]

\[\angle BEC = 180 - 60 = 120{^\circ};\]

\[\angle EBC = \angle ECB =\]

\[= \frac{1}{2}(180 - 120) = 30{^\circ}.\]

\[4)\ ⊿ADC - равнобедренный:\]

\[\angle DAC = \angle DCA = 30{^\circ};\]

\[\angle ADC = 120{^\circ}.\]

\[5)\ По\ теореме\ синусов:\]

\[\frac{\text{AD}}{\sin{30{^\circ}}} = \frac{\text{AC}}{\sin{120{^\circ}}}\]

\[AD = \frac{\sin{30{^\circ}}}{\sin{120{^\circ}}} \cdot AC = \frac{1}{2}\ :\frac{\sqrt{3}}{2} \cdot 6 =\]

\[= 2\sqrt{3}.\]

\[Ответ:2\sqrt{3}.\]

\[\boxed{\mathbf{5.}}\]

\[Дано:\]

\[CH = AB.\]

\[Найти:\]

\[\angle ACB.\]

\[Решение.\]

\[1)\ ⊿CHB_{1}\ подобен\ ⊿BHC_{1}:\]

\[\angle CB_{1}H = \angle BC_{1}H = 90{^\circ};\]

\[\angle CHB_{1} = \angle BHC_{1} - как\ \]

\[вертикальные.\]

\[Отсюда:\]

\[\angle B_{1}CH = \angle HBC_{1}.\]

\[2)\ ⊿CB_{1}H = ⊿BB_{1}A - по\ \]

\[гипотенузе\ и\ острому\ углу:\]

\[\angle B_{1}CH = \angle B_{1}BA;\]

\[CH = AB.\]

\[Отсюда:\]

\[CB_{1} = BB_{1}.\]

\[3)\ Прямоугольный\ ⊿CBB_{1} -\]

\[равнобедренный:\]

\[CB_{1} = BB_{1}.\]

\[Отсюда:\]

\[\angle ACB = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{6.}}\]

\[Решение.\]

\[Точки\ \text{M\ }и\ \text{N\ }лежат\ на\ \]

\[окружности\ диаметром\ \text{BC.}\]

\[Первый\ случай:\ \angle A - острый.\]

\[⊿AMN\ подобен\ ⊿ABC:\]

\[k = \frac{\text{MN}}{\text{BC}} = \frac{12}{24} = \frac{1}{2}.\]

\[Отсюда:\]

\[\angle A = 60{^\circ};\ \ \angle BOC = 120{^\circ}.\]

\[По\ теореме\ синусов\ найдем\ \]

\[радиус\ описанной\ окружности\ \]

\[⊿BOC:\]

\[R = \frac{\text{BC}}{2\sin{\angle BOC}} = \frac{24}{2\sin{120{^\circ}}} =\]

\[= \frac{24}{2 \cdot \frac{\sqrt{3}}{2}} = 8\sqrt{3}.\]

\[Второй\ случай:\ \angle A - тупой.\]

\[\cos{\angle CAN} = \frac{1}{2}:\]

\[\angle CAN = 60{^\circ};\]

\[\angle A = 120{^\circ};\]

\[\angle BOC = 150{^\circ}.\]

\[R = \frac{24}{2\sin{150{^\circ}}} = \frac{24}{2 \cdot \frac{1}{2}} = 24.\]

\[Ответ:8\sqrt{3}\ или\ \ 24.\]

\[\boxed{\mathbf{7.}}\]

\[Рассмотрим\ разные\ виды\ \]

\[треугольника,\ связанные\ с\ \]

\[выбором\ острого\ или\ тупого\ \]

\[угла.\]

\[1.\ ⊿ABC - остроугольный.\]

\[⊿BC_{1}A_{1}\ подобен\ ⊿ABC:\]

\[\angle BC_{1}A_{1} = \angle BCA.\]

\[⊿AB_{1}C_{1}\ подобен\ ⊿ABC:\]

\[\angle AC_{1}B_{1} = \angle BCA.\]

\[Развернутый\ угол\ при\ вершине\ \]

\[C_{1} =\]

\[= \angle BC_{1}A_{1} + \angle AC_{1}B_{1} + \angle B_{1}C_{1}A_{1}:\]

\[2\angle C + \angle B_{1}C_{1}A_{1} = 180{^\circ}\]

\[\angle C = 90{^\circ} - \frac{1}{2}\angle B_{1}C_{1}A_{1}.\]

\[Такие\ же\ равенства\ получаем\ \]

\[из\ других\ острых\ углов.\]

\[90{^\circ} - \frac{1}{2} \cdot 90{^\circ} = 45{^\circ};\]

\[90{^\circ} - \frac{1}{2} \cdot 60{^\circ} = 60{^\circ};\]

\[90{^\circ} - \frac{1}{2} \cdot 30{^\circ} = 75{^\circ}.\]

\[2.\ \angle ACB - тупой.\]

\[\angle A = \frac{\angle A_{1}}{2} = \frac{90}{2} = 45{^\circ};\]

\[\angle B = \frac{\angle B_{1}}{2} = \frac{60}{2} = 30{^\circ};\]

\[\angle C = 180 - (45 + 30) = 105{^\circ}.\]

\[3.\ \angle ABC - тупой.\]

\[\angle A = \frac{\angle A_{1}}{2} = \frac{90}{2} = 45{^\circ};\]

\[\angle C = \frac{\angle C_{1}}{2} = \frac{30}{2} = 15{^\circ};\]

\[\angle B = 180 - (45 + 15) = 120{^\circ}.\]

\[4.\ \angle\text{BAC} - тупой.\]

\[\angle B = \frac{\angle B_{1}}{2} = \frac{60}{2} = 30{^\circ};\]

\[\angle C = \frac{\angle C_{1}}{2} = \frac{30}{2} = 15{^\circ};\]

\[\angle A = 180{^\circ} - (30 + 15) = 135{^\circ}.\]

\[\boxed{\mathbf{8.}}\]

\[Дано:\]

\[Найти:\]

\[\frac{\text{MN}}{\text{KN}}.\]

\[Решение.\]

\[H - ортоцентр\ ⊿ABC:\]

\[H - точка\ пересечения\ \]

\[биссектрис\ и\ центр\ вписанной\ \]

\[в\ ⊿MNK\ окружности.\]

\[Найдем\ углы\ ⊿MNK:\]

\[\angle M = 2 \cdot (90{^\circ} - \angle A) =\]

\[= 2 \cdot (90 - 45) = 90{^\circ};\]

\[\angle K = 2 \cdot (90{^\circ} - \angle C) =\]

\[= 2 \cdot (90 - 60) = 60{^\circ};\]

\[\angle N = 180{^\circ} - (90{^\circ} + 60{^\circ}) = 30{^\circ}.\]

\[Отсюда:\]

\[\frac{\text{MN}}{\text{KN}} = \cos{30{^\circ}} = \frac{\sqrt{3}}{2}.\]

\[Ответ:\frac{\sqrt{3}}{2}.\]

\[\boxed{\mathbf{9.}}\]

\[Дано:\]

\[BM - медиана;\]

\[\frac{\sin{\angle ABM}}{\sin{\angle CBM}} = \frac{1}{2}.\]

\[Найти:\]

\[\frac{\text{BC}}{\text{AB}}.\]

\[Решение.\]

\[По\ теореме\ синусов\ (⊿ABM):\]

\[\frac{\text{AB}}{\sin{\angle BMA}} = \frac{\text{AM}}{\sin{\angle ABM}}.\]

\[По\ теореме\ синусов\ (⊿CBM):\]

\[\frac{\text{BC}}{\sin{\angle BMC}} = \frac{\text{MC}}{\sin{\angle CBM}}.\]

\[AM = MC;\ \sin{\angle BMA} =\]

\[= \sin{(180{^\circ} - \angle BMA}) =\]

\[= \sin{\angle BMC}:\]

\[AM \cdot \sin{\angle BMA} =\]

\[= AB \cdot \sin{\angle ABM};\]

\[MC \cdot \sin{\angle BMC} = BC \cdot \sin{\angle CBM};\]

\[AM \cdot \sin{\angle BMA} = MC \cdot \sin{\angle BMC}\]

\[AB \cdot \sin{\angle ABM} = BC \cdot \sin{\angle CBM}\]

\[\frac{\text{BC}}{\text{AB}} = \frac{\sin{\angle ABM}}{\sin{\angle CBM}} = \frac{1}{2}.\]

\[Ответ:\ \frac{1}{2}.\]

\[\boxed{\mathbf{10.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ продолжения\ отрезков\ \]

\[BN\ и\ AD\ пересекаются\ в\ \]

\[точке\ E.\ \]

\[⊿DNE = ⊿CNB - по\ стороне\ и\ \]

\[прилежащим\ к\ ней\ углам:\]

\[DE\ = \ BC\ = \ 2BM;\ \ \]

\[AE\ = \ 4a.\ \]

\[Треугольник\ BOM\ подобен\ \]

\[треугольнику\ EOA:\ \ \]

\[MO\ :\ OA\ = \ 1\ :\ 4.\]

\[Ответ:\ \ 1\ :4.\]

\[\boxed{\mathbf{11.}}\]

\[Пусть\ ABCD\ —\ данная\ \]

\[трапеция;\ \]

\[AB\ и\ CD\ —\ ее\ основания\ \]

\[(AB\ < \ CD);\ \]

\[M,\ N\ —\ середины\ AB\ и\ CD\ \]

\[соответственно.\ \]

\[Пусть\ \angle ADC\ = \ 50{^\circ};\ \]

\[\angle BCD\ = \ 40{^\circ}.\]

\[Средняя\ линия\ трапеции\ равна\ \]

\[полусумме\ оснований:\]

\[AB\ + \ CD\ = \ 8.\ \]

\[Продлим\ боковые\ стороны\ \]

\[DA\ и\ CB\ до\ пересечения\ в\ \]

\[точке\ E.\ \]

\[Рассмотрим\ треугольник\ ABE,\ \]

\[в\ котором\ \angle EAB\ = \ 50{^\circ};\ \]

\[\angle EBA\ = \ 40{^\circ}:\]

\[\ \angle AEB\ = \ 90{^\circ}.\ \]

\[Медиана\ EM\ этого\ \]

\[треугольника,\ проведенная\ из\ \]

\[вершины\ прямого\ угла,\ равна\ \]

\[половине\ гипотенузы:\ \]

\[EM\ = \ AM.\ \]

\[Пусть\ EM\ = \ x,\ тогда\ AM\ = \ x,\ \]

\[DN\ = \ 4\ –\ x.\ \]

\[\ MN\ = \ 1:\]

\[EN\ = \ x\ + \ 1.\ \]

\[Из\ подобия\ треугольников\ \]

\[AEM\ и\ DEN:\]

\[\frac{\text{AM}}{\text{DN}} = \frac{\text{EM}}{\text{EN}}\]

\[\frac{x}{4 - x} = \frac{x}{x + 1}\]

\[x = \frac{3}{2}.\]

\[Отсюда:\]

\[AB = 3;\ \ CD = 5.\]

\[Ответ:3\ и\ 5\ .\]

\[\boxed{\mathbf{12.}}\]

\[Дано:\]

\[Решение.\]

\[Из\ вершины\ C\ меньшего\ \]

\[основания\ равнобедренной\ \]

\[трапеции\ ABCD\ опустим\ \]

\[перпендикуляр\ CM\ на\ большее\ \]

\[основание.\ \]

\[Тогда\ отрезок\ AK\ равен\ \]

\[полусумме\ оснований\ \]

\[трапеции.\ \]

\[В\ прямоугольном\ треугольнике\ \]

\[AKC\ катет\ AK\ лежит\ против\ \]

\[угла\ в\ 30{^\circ}:\ \]

\[AK = \frac{1}{2}AC = \frac{1}{2} \cdot 10 = 5.\]

\[Средняя\ линия\ MN\ трапеции\ \]

\[равна\ полусумме\ оснований:\]

\[MN = AK = 5.\]

\[Ответ:5.\]

\[\boxed{\mathbf{13.}}\]

\[Решение.\]

\[Середины\ сторон\ любого\ \]

\[четырёхугольника\ являются\ \]

\[вершинами\ параллелограмма,\ \]

\[стороны\ которого\ \]

\[параллельны\ диагоналям\ \]

\[четырёхугольника\ и\ \]

\[соответственно\ равны\ их\ \]

\[половинам.\ \]

\[Обозначим\ через\ x\ и\ 3x\ \]

\[половины\ диагоналей\ \]

\[параллелограмма.\ \]

\[Поскольку\ угол\ между\ ними\ \]

\[равен\ 60{^\circ},\ то\ по\ теореме\ \]

\[косинусов:\]

\[x^{2} + 9x^{2} - 3x^{2} = 7x^{2}\]

\[x^{2} + 9x^{2} + 3x^{2} = 13x^{2}.\]

\[Так\ как\ большая\ сторона\ \]

\[четырехугольника\ равна\ \sqrt{39},\]

\[то\ большая\ сторона\ \]

\[параллелограмма\ равна\ \frac{\sqrt{39}}{2}:\]

\[13x^{2} = \frac{39}{4}\]

\[x^{2} = \frac{3}{4}\]

\[x = \frac{\sqrt{3}}{2}.\]

\[Меньшая\ сторона\ \]

\[параллелограмма:\]

\[x\sqrt{7} = \frac{\sqrt{3}}{2} \cdot \sqrt{7} = \frac{\sqrt{21}}{2}.\]

\[Меньшая\ диагональ\ данного\ \]

\[четырехугольника:\]

\[\sqrt{21}.\]

\[Ответ:\sqrt{21}.\]

\[\boxed{\mathbf{14.}}\]

\[Решение.\]

\[1)\cos{\angle BCD} = - \frac{2}{7}:\]

\[\angle BCD - тупой;\]

\[\angle ADC - острый;\]

\[\cos{\angle ADC} = \frac{2}{7}.\]

\[2)\ Проведем\ CH\bot AD:\]

\[DH = CD \cdot \cos{\angle ADC} = 28 \cdot \frac{2}{7} =\]

\[= 8;\]

\[CH = CD \cdot \sin{\angle ADC} =\]

\[= 28 \cdot \sqrt{1 - \frac{4}{49}} = 28 \cdot \frac{\sqrt{45}}{7} =\]

\[= 4 \cdot 3\sqrt{5} = 12\sqrt{5}.\]

\[3)\ Через\ вершину\ C\ проведём\ \]

\[прямую,\ параллельную\ \]

\[боковой\ стороне\ AB\ ,\ до\ \]

\[пересечения\ с\ прямой\ AD\ в\ \]

\[точке\ P:\]

\[PH = \sqrt{CP^{2} - CH^{2}} =\]

\[= \sqrt{AB^{2} - CH^{2}} =\]

\[= \sqrt{27^{2} - \left( 12\sqrt{5} \right)^{2}} = 3.\]

\[\textbf{а)}\ Точка\ \text{P\ }лежит\ между\ \text{A\ }и\ H:\]

\[AH = AP + PH = 5 + 3 = 8;\]

\[AC = \sqrt{AH^{2} + CH^{2}} =\]

\[= \sqrt{64 + 144 \cdot 5} = \sqrt{784} = 28.\]

\[\textbf{б)}\ Точка\ \text{P\ }лежит\ между\ \text{D\ }и\ H:\]

\[AH = AP - PH = 5 - 3 = 2;\]

\[AC = \sqrt{AH^{2} + CH^{2}} =\]

\[= \sqrt{4 + 144 \cdot 5} = \sqrt{724}.\]

\[Ответ:28\ или\ \sqrt{724}.\]

\[\boxed{\mathbf{15.}}\]

\[Дано:\]

\[Решение.\]

\[Обозначим\ через\ A\ и\ B\ точки\ \]

\[пересечения\ прямой\ c\ с\ \]

\[параллельными\ прямыми\ a\ и\ b\ \]

\[соответственно.\ \]

\[Пусть\ окружность\ с\ центром\ O\ \]

\[касается\ прямых\ a\ и\ b\ \]

\[соответственно\ в\ точках\ M\ и\ N.\ \]

\[Тогда\ AO\ –\ биссектриса\ угла\ \]

\[BAM,\ а\ BO\ –\ биссектриса\ угла\ \]

\[\text{ABN.\ }\]

\[Поскольку\ \angle BAM + \angle ABN =\]

\[= 180{^\circ}:\]

\[\angle BAO + \angle ABO =\]

\[= \frac{1}{2}\angle BAM + \frac{1}{2}\angle ABN =\]

\[= \frac{1}{2}(\angle BAM + \angle ABN) =\]

\[= \frac{1}{2} \cdot 180{^\circ} = 90{^\circ}.\]

\[Отсюда:\]

\[\angle AOB =\]

\[= 180{^\circ} - (\angle BAO + \angle ABO) = 90{^\circ}.\]

\[Ответ:90{^\circ}.\]

\[\boxed{\mathbf{16.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ E\ —\ точка\ пересечения\ \]

\[окружности\ с\ отрезком\ OM:\ \]

\[OM = 2OE = 2R\ .\ \]

\[В\ прямоугольном\ треугольнике\ \]

\[OAM\ катет\ OA\ вдвое\ меньше\ \]

\[гипотенузы\ OM:\ \ \]

\[\angle AMO\ = \ 30{^\circ}.\]

\[MO\ —\ биссектриса\ угла\ AMC:\]

\[\angle AMC = 60{^\circ}.\ \]

\[Из\ прямоугольного\ \]

\[треугольника\ MAC:\]

\[\angle ACM\ = \ 30{^\circ}.\]

\[Значит:\]

\[⊿MOC\ —\ равнобедренный.\ \]

\[Следовательно:\]

\[OC = OM\ = \ 2R.\]

\[Ответ:2R.\]

\[\boxed{\mathbf{17.}}\]

\[Решение.\]

\[Расстояния\ от\ центра\ \]

\[окружности\ до\ данных\ хорд:\]

\[\sqrt{25^{2} - 20^{2}} = \sqrt{5 \cdot 45} =\]

\[= \sqrt{25 \cdot 9} = 15;\]

\[\sqrt{25^{2} - 7^{2}} = \sqrt{18 \cdot 32} =\]

\[= \sqrt{36 \cdot 16} = 24.\]

\[1)\ Если\ хорды\ расположены\ по\ \]

\[разные\ стороны\ от\ центра:\]

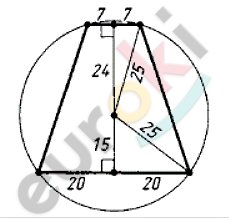
\[24 + 15 = 39 - расстояние\ \]

\[между\ ними.\]

\[2)\ Если\ хорды\ расположены\ по\ \]

\[одну\ сторону\ от\ центра:\]

\[24 - 15 = 9 - расстояние\ \]

\[между\ ними.\]

\[Ответ:39\ или\ 9.\]

\[\boxed{\mathbf{18.}}\]

\[Дано:\]

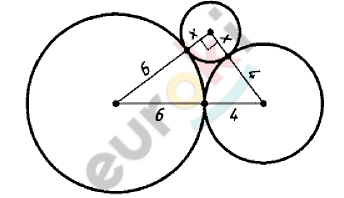
\[Решение.\]

\[Пусть\ x - радиус\ меньше\ \]

\[окружности.\]

\[Стороны\ получившегося\ \]

\[треугольника:\ \]

\[10;\ \ 6 + x;\ \ 4 + x.\]

\[Наибольшая\ сторона\ равна\ \]

\[10 - это\ гипотенуза.\]

\[По\ теореме\ Пифагора:\]

\[(x + 6)^{2} + (x + 4)^{2} = 100\]

\[x^{2} + 12x + 36 + x^{2} + 8x + 16 - 100 =\]

\[= 0\]

\[2x^{2} + 20x - 48 = 0\ \ \ |\ :2\]

\[x^{2} + 10x - 24 = 0\]

\[D_{1} = 25 + 24 = 49\]

\[x_{1} = - 5 - 7 =\]

\[= - 12\ (не\ подходит);\]

\[x_{2} = - 5 + 7 = 2 - радиус\ \]

\[меньшей\ окружности.\]

\[Ответ:2.\]

\[\boxed{\mathbf{19.}}\]

\[Дано:\]

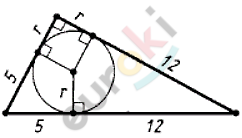
\[Решение.\]

\[Пусть\ r - радиус\ вписанной\ \]

\[окружности.\]

\[Тогда\ катеты\ треугольника:\]

\[5 + r;\ \ 12 + r.\]

\[По\ теореме\ Пифагора:\]

\[(5 + r)^{2} + (12 + r)^{2} = (5 + 12)^{2}\]

\[25 + 10r + r^{2} + 144 + 24r + r^{2} =\]

\[= 289\]

\[2r^{2} + 34r - 120 = 0\ \ |\ :2\]

\[r^{2} + 17r - 60 = 0\]

\[r_{1} + r_{2} = - 17;\ \ r_{1} \cdot r_{2} = - 60\]

\[r_{1} = - 20\ (не\ подходит);\]

\[r_{2} = 3 - радиус\ вписанной\ \]

\[окружности.\]

\[5 + r = 5 + 3 = 8 - один\ катет.\]

\[12 + r = 12 + 3 = 15 - другой\ \]

\[катет.\]

\[Ответ:8\ и\ 15.\]

\[\boxed{\mathbf{20.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ линия\ центров\ O_{1}O_{2}\ \]

\[пересекает\ общую\ хорду\ AB\ \]

\[окружностей\ в\ точке\ M.\ \]

\[Тогда\ M\ —\ середина\ AB\ и\ \]

\[O_{1}O_{2}\bot AB.\]

\[⊿AO_{1}B\ —\ прямоугольный\ и\ \]

\[равнобедренный;\]

\[⊿AO_{2}B\ —\ равносторонний.\]

\[Если\ r\ и\ R\ —\ радиусы\ \]

\[окружностей\ с\ центрами\ \]

\[O_{1}\ и\ O_{2}\ соответственно:\]

\[AB = r\sqrt{2};\ \ \ AB = R;\]

\[R = r\sqrt{2}.\]

\[Отсюда:\]

\[O_{1}M = \frac{r\sqrt{2}}{2};\]

\[O_{2}M = \frac{R\sqrt{3}}{2} = \frac{r\sqrt{2} \cdot \sqrt{3}}{2} = \frac{r\sqrt{6}}{2}.\]

\[Центры\ окружностей\ лежат\ по\ \]

\[разные\ стороны\ от\ прямой\ AB:\]

\[O_{1}M + MO_{2} = O_{1}O_{2}\]

\[\frac{r\sqrt{2}}{2} + \frac{r\sqrt{6}}{2} = a\]

\[r = \frac{a\sqrt{2}}{\sqrt{3} + 1\ };\ \ \]

\[R = r\sqrt{2} = \frac{2a}{\sqrt{3} + 1}.\]

\[Ответ:\ \ \frac{a\sqrt{2}}{\sqrt{3} + 1\ };\ \ \frac{2a}{\sqrt{3} + 1}.\]

\[\boxed{\mathbf{21.}}\]

\[Дано:\]

\[Решение.\]

\[⊿AO_{1}B - равнобедренный,\ \]

\[с\ основанием\ AB;\]

\[⊿BO_{2}C - равнобедренный,\ \]

\[с\ основанием\ \text{BC.}\]

\[⊿AO_{1}\text{B\ }подобен\ BO_{2}C - по\ \]

\[двум\ углам:\]

\[\angle ABO_{1} = \angle CBO_{2} - как\ \]

\[вертикальные;\]

\[\angle BAO_{1} = \angle ABO_{1} = \angle CBO_{2} =\]

\[= \angle BCO_{2}.\]

\[Из\ подобия\ треугольников:\]

\[\frac{\text{AB}}{\text{BC}} = \frac{O_{1}A}{O_{2}B} = \frac{r_{1}}{r_{2}} = \frac{2}{4} = \frac{1}{2};\]

\[BC = \frac{2}{3}AC = \frac{2}{3} \cdot 3\sqrt{2} = 2\sqrt{2}.\]

\[Ответ:2\sqrt{2}.\]

\[\boxed{\mathbf{22.}}\]

\[Решение.\]

\[1)\ Рассмотрим\ случай\ \]

\[внешнего\ касания.\ \]

\[Пусть\ O_{1}\ и\ O_{2}\ —\ центры\ \]

\[окружностей\ S_{1}\ и\ S_{2};\ \]

\[X\ —\ точка\ пересечения\ прямой\ \]

\[AB\ с\ окружностью\ S_{2},\ отличная\ \]

\[от\ A;\ \]

\[BM\ —\ касательная\ к\ \]

\[окружности\ S_{1}\ \]

\[(M\ —\ точка\ касания).\]

\[Равнобедренные\ треугольники\ \]

\[XO_{2}A\ и\ BO_{1}A\ подобны:\]

\[AX = \frac{r}{R} \cdot AB = \frac{\text{ar}}{R}.\]

\[По\ теореме\ о\ касательной\ и\ \]

\[секущей:\]

\[BM^{2} = BX \cdot BA =\]

\[= (BA + AX) \cdot BA =\]

\[= \left( a + \frac{\text{ar}}{R} \right) \cdot a = a^{2}\left( 1 + \frac{r}{R} \right)\]

\[BM = a\sqrt{1 + \frac{r}{R}}.\]

\[2)\ Аналогично\ в\ случае\ \]

\[внутреннего\ касания.\]

\[BM = a\sqrt{1 - \frac{r}{R}}.\]

\[Ответ:\ a\sqrt{1 + \frac{r}{R}};\ a\sqrt{1 - \frac{r}{R}}\text{.\ \ }\]

\[\boxed{\mathbf{23.}}\]

\[Дано:\]

\[\angle OAK = 60{^\circ}.\]

\[Решение.\]

\[Возможны\ два\ случая.\]

\[1)\ C - центр\ искомой\ \]

\[окружности;r - искомый\ \]

\[радиус.\]

\[CT\bot OA.\]

\[⊿CTO - прямоугольный:\]

\[OC = 2 + r;\]

\[CT = r.\]

\[⊿CTA - прямоугольный:\]

\[\angle CAT = \frac{\angle OAK}{2} = 30{^\circ};\]

\[TA = \frac{\text{CT}}{tg\ 30{^\circ}} = r \cdot \sqrt{3}.\]

\[В\ ⊿OAK:\]

\[OA = \frac{4}{\sqrt{3}};\]

\[OT = OA - TA = \frac{4}{\sqrt{3}} - r\sqrt{3}.\]

\[Теорема\ Пифагора\ (⊿CTO):\]

\[r^{2} + \left( \frac{4}{\sqrt{3}} - \frac{r}{\sqrt{3}} \right)^{2} = (r + 2)^{2}.\]

\[2)\ Для\ второго\ случая\ \]

\[уравнение\ будет\ таким\ же.\ \]

\[Приводим:\]

\[9r^{2} - 36r + 4 = 0\]

\[D_{1} = 324 - 36 = 288\]

\[r = \frac{18 \pm \sqrt{288}}{9} = \frac{18 \pm 12\sqrt{2}}{9} =\]

\[= 2 \pm \frac{4\sqrt{2}}{3}\text{.\ }\]

\[Ответ:\ 2 - \frac{4\sqrt{2}}{3}\ или\ 2 + \frac{4\sqrt{2}}{3}.\]

\[\boxed{\mathbf{24.}}\]

\[Решение.\]

\[Пусть\ O_{1} - центр\ окружности\ \]

\[радиуса\ R;\]

\[O_{2} - центр\ окружности\ \]

\[радиуса\ \text{r.}\]

\[Возможны\ два\ случая.\]

\[1)\ AB - внешняя\ касательная:\]

\[через\ точку\ O_{2}\ проведем\ \]

\[прямую,\ \parallel AB;\]

\[P - точка\ ее\ пересечения\ с\ \]

\[прямой\ O_{1}\text{A.}\]

\[Отсюда:\]

\[AB = \sqrt{O_{1}O_{2}^{2} - O_{1}P^{2}} =\]

\[= \sqrt{a^{2} - (R - r)^{2}}.\]

\[2)\ AB - внутренняя\ \]

\[касательная:\]

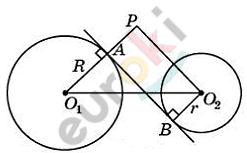
\[через\ точку\ O_{2}\ проведем\ \]

\[прямую,\ \parallel AB;\]

\[P - точка\ ее\ пересечения\ с\ \]

\[прямой\ O_{1}\text{A.}\]

\[Отсюда:\]

\[AB = \sqrt{O_{1}O_{2}^{2} - O_{1}P^{2}} =\]

\[= \sqrt{a^{2} - (R + r)^{2}}.\]

\[Ответ:\ \ \sqrt{a^{2} - (R - r)^{2}};\ \]

\[\sqrt{a^{2} - (R + r)^{2}}.\]

\[\boxed{\mathbf{25.}}\]

\[Решение.\]

\[Два\ возможных\ случая.\]

\[1)\ Если\ точки\ O\ и\ B\ лежат\ по\ \]

\[разные\ стороны\ от\ прямой\ AC,\ \]

\[то\ градусная\ мера\ дуги\ AC\ ,\ \]

\[не\ содержащей\ точки\ B\ ,\ равна:\]

\[360{^\circ} - 60{^\circ} = 300{^\circ}.\]

\[\angle ABC = \frac{1}{2} \cdot 300{^\circ} = 150{^\circ}.\]

\[Сумма\ углов\ при\ вершинах\ \]

\[A\ и\ C\ треугольника\ ABC\ равна:\]

\[180{^\circ} - 150{^\circ} = 30{^\circ}.\]

\[AM\ и\ CM\ —\ биссектрисы\ \]

\[треугольника\ ABC\ ,\ то\ сумма\ \]

\[углов\ при\ вершинах\ A\ и\ C\ \]

\[треугольника\ AMC\ равна\ 15{^\circ}.\]

\[Отсюда:\]

\[\angle AMC = 180{^\circ} - 15{^\circ} = 165{^\circ}.\]

\[2)\ Если\ точки\ O\ и\ B\ лежат\ по\ \]

\[одну\ сторону\ от\ прямой\ AC,\ то\ \]

\[аналогично\ получим:\]

\[\angle AMC = 105{^\circ}.\]

\[Ответ:165{^\circ}\ или\ 105{^\circ}.\]

\[\boxed{\mathbf{26.}}\]

\[Решение.\]

\[По\ теореме\ синусов:\]

\[\frac{6}{\sin C} = \frac{4}{\sin A} = 24;\]

\[\sin C = \frac{1}{4};\ \sin A = \frac{1}{6}.\]

\[Возможны\ два\ случая\ \]

\[расположения\ вершин\ \text{C\ }\]

\[треугольника\ \text{ABC.}\]

\[1)\ \]

\[2)\ \]

\[Опустим\ BH\bot AC:\]

\[BH = AB \cdot \sin A = 1.\]

\[По\ теореме\ Пифагора:\]

\[AH = \sqrt{6^{2} - 1} = \sqrt{35};\]

\[CH = \sqrt{4^{2} - 1} = \sqrt{15}.\]

\[В\ первом\ случае:\]

\[AC = \sqrt{35} + \sqrt{15}.\]

\[Во\ втором\ случае:\]

\[AC = \sqrt{35} - \sqrt{15}.\]

\[Ответ:\ \sqrt{35} + \sqrt{15}\ или\ \]

\[\sqrt{35} - \sqrt{15}.\]

\[\boxed{\mathbf{27.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ CD\ —‍\ общая\ хорда\ \]

\[окружностей,\ построенных\ на\ \]

\[катетах\ AC\ = \ 3‍\ и\ BC\ = \ 4‍\ \]

\[прямоугольного\ треугольника\ \]

\[ABC‍,\ как\ на\ диаметрах.\ \]

\[Тогда\ \angle ADC = \angle BDC = 90{^\circ} -\]

\[как\ вписанные\ углы,\ \]

\[опирающиеся\ на\ диаметр.\ \]

\[Значит,\ точка\ D‍\ лежит\ на\ \]

\[гипотенузе\ AB;\ \]

\[CD\ —‍\ высота\ прямоугольного\ \]

\[треугольника\ ABC,‍\ \]

\[проведённая\ из\ вершины\ \]

\[прямого\ угла.\]

\[По\ теореме\ Пифагора:\]

\[AB = \sqrt{9 + 16} = 5.\]

\[S_{\text{ABC}} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD:\]

\[\frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD\]

\[CD = \frac{AC \cdot BC}{\text{AB}} = \frac{3 \cdot 4}{5} = \frac{12}{5}.\]

\[Ответ:\ \frac{12}{5}.\]

\[\boxed{\mathbf{28.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ CD\ —‍\ высота\ \]

\[равнобедренного\ треугольника\ \]

\[ABC‍\ со\ сторонами\ AC\ = \ BC\ = \ \]

\[= 13‍\ и\ AB\ = \ 24;‍\]

\[\ O\ —‍\ центр\ его\ описанной\ \]

\[окружности\ радиуса\ R;‍\]

\[\ Q\ —‍\ центр\ вписанной\ \]

\[окружности\ радиуса\ r.‍\ \]

\[Из\ прямоугольного\ \]

\[треугольника\ ACD‍\ находим:\]

\[CD = \sqrt{AC^{2} - AD^{2}} =\]

\[= \sqrt{13^{2} - 12^{2}} = 5.\]

\[\sin{\angle CAD} = \frac{\text{CD}}{\text{AC}} = \frac{5}{13}.\]

\[По\ теореме\ синусов:\]

\[R = \frac{\text{BC}}{2\sin{\angle BAC}} = \frac{13}{2 \cdot \frac{5}{13}} =\]

\[= \frac{169}{10} = 16,9.\]

\[Радиус\ окружности,\ вписанной\ \]

\[в\ треугольник,\ равен\ площади\ \]

\[треугольника,\ делённой\ на\ его\ \]

\[полупериметр:\]

\[r = \frac{S_{\text{ABC}}}{AC + AD} = \frac{AD \cdot CD}{AC + AD} =\]

\[= \frac{12 \cdot 5}{13 + 12} = 2,4.\]

\[Угол\ CAD‍\ меньше\ 45‍{^\circ},‍\ так\ как\ \]

\[его\ тангенс\ меньше\ \]

\[1\ \left( \text{tg}\angle CAD = \frac{5}{12} < 1 \right):\]

\[\angle ACB - тупой;\ \ \]

\[точки\ \text{O\ }и\ \text{Q\ }лежат\ по\ разные\ \]

\[стороны\ от\ прямой\ \text{AB.}\]

\[Следовательно:\]

\[OQ = OC - CQ =\]

\[= OC - (CD - QD) =\]

\[= R - (CD - r) =\]

\[= 16,9 - (5 - 2,4) = 14,3.\]

\[Ответ:2,4;16,9;14,3.\]

\[\boxed{\mathbf{29.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ O_{1}\ и\ O_{2} - центры\ \]

\[окружностей\ S_{1}\ и\ S_{2}\ \]

\[соответственно.\]

\[Тогда:\]

\[\angle AO_{1}C = 360{^\circ} \cdot \frac{5}{5 + 7} = 150{^\circ}.\]

\[\angle O_{2}AC = 90{^\circ} - радиус,\ \]

\[проведённый\ в\ точку\ касания,\ \]

\[перпендикулярен\ касательной;\]

\[O_{2}C - диаметр\ окружности\ S_{1}:\]

\[\angle AO_{2}C = \frac{1}{2}\angle AO_{1}C = 75{^\circ}.\]

\[Тогда\ градусная\ мера\ дуги\ \]

\[окружности\ S‍_{2},‍\ заключённой\ \]

\[между\ сторонами\ угла\ AO‍_{2}C,‍\ \]

\[равна\ 75{^\circ};\]

\[градусная\ мера\ дуги\ AB‍\ \]

\[окружности\ S‍_{2},‍\ содержащейся\ \]

\[внутри\ окружности\ S‍_{1},‍\ равна\ \]

\[150‍{^\circ}.\]

\[Следовательно,\ \]

\[дополнительная\ к\ ней\ дуга\ \]

\[окружности\ S‍_{2}‍\ равна:\]

\[360{^\circ} - 150{^\circ} = 210{^\circ}.\]

\[Ответ:150{^\circ}\ и\ 210{^\circ}.\]

\[\boxed{\mathbf{30.}}\]

\[Решение.\]

\[Возможны\ два\ случая.\]

\[1)\ Точка\ касания\ на\ луче\ \text{BC.}\]

\[O - центр\ окружности;он\ \]

\[лежит\ на\ срединном\ \]

\[перпендикуляре:\]

\[PO\bot AD;\]

\[OE\bot BC.\]

\[O - середина\ AB:\]

\[OE = OB \cdot \sin{30{^\circ}} = 2 \cdot \frac{1}{2} = 1;\]

\[OE = OA = OB = R = 1.\]

\[2)\ Точка\ касания\ на\ \]

\[продолжении\ луча\ \text{BC.}\]

\[OE = OA = OB = R.\]

\[По\ теореме\ о\ касательной\ и\ \]

\[секущей:\]

\[BE^{2} = BD \cdot BA = 1 \cdot 3 = 3;\]

\[BE = \sqrt{3}.\]

\[F - середина\ \text{AD.}\]

\[⊿AOD - равнобедренный:\]

\[OF - медина,\ высота\ и\ \]

\[биссектриса.\]

\[Продолжим\ \text{OF\ }до\ пересечения\ \]

\[с\ BC:\]

\[H - точка\ пересечения.\]

\[OH\bot BA;\ \ OE\bot BC:\]

\[\angle HOE = \angle ABC = 30{^\circ}.\]

\[Отсюда:\]

\[EH = OE \cdot tg\ 30{^\circ} = \frac{R}{\sqrt{3}}.\]

\[С\ другой\ стороны:\]

\[EH = EB + BH = \sqrt{3} + \frac{\text{BF}}{\cos{30{^\circ}}} =\]

\[= \sqrt{3} + \frac{2}{\sqrt{3}} \cdot 2 = \sqrt{3} + \frac{4}{\sqrt{3}}.\]

\[Получаем:\]

\[\frac{R}{\sqrt{3}} = \sqrt{3} + \frac{4}{\sqrt{3}}\]

\[R = 3 + 4 = 7.\]

\[Ответ:1\ или\ 7.\]

\[\boxed{\mathbf{31.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ O_{1}\ и\ O_{2}\ —\ центры\ \]

\[окружностей,\ вписанных\ в\ \]

\[треугольники\ ADC\ и\ ABD\ \]

\[соответственно;\ \]

\[P\ и\ Q\ —\ их\ точки\ касания\ со\ \]

\[стороной\ BC.\]

\[Пусть\ \angle ADB = \alpha.\]

\[В\ равнобедренном\ ⊿ADB:\]

\[\sin\frac{\alpha}{2} = \frac{4}{5};\ \ \cos\frac{\alpha}{2} = \frac{3}{5};\]

\[DQ = \frac{DB + AD + AB}{2} - AB = \frac{1}{2}.\]

\[Аналогично:\]

\[DP = 1.\]

\[Тогда:\]

\[DO_{2} = \frac{\text{DQ}}{\cos\frac{\alpha}{2}} = \frac{5}{6};\]

\[DO_{1} = \frac{\text{DP}}{\cos\left( 90{^\circ} - \frac{\alpha}{2} \right)} = \frac{\text{DP}}{\sin\frac{\alpha}{2}} =\]

\[= \frac{5}{4};\]

\[O_{1}O_{2} = \sqrt{DO_{1}^{2} + DO_{2}^{2}} =\]

\[= \sqrt{\left( \frac{5}{4} \right)^{2} + \left( \frac{5}{6} \right)^{2}} = \sqrt{\frac{325}{144}} =\]

\[= \frac{5\sqrt{13}}{12}.\]

\[Ответ:\frac{5\sqrt{13}}{12}.\]

\[\boxed{\mathbf{32.}}\]

\[Дано:\]

\[Решение.\ \]

\[Пусть\ M\ —‍\ точка\ пересечения\ \]

\[отрезка\ AB‍\ с\ общей\ \]

\[касательной\ к\ данным\ \]

\[окружностям,\ проведённой\ \]

\[через\ их\ точку\ касания\ C:\]

\[MA = MC = MB;\]

\[\angle ACB = 90{^\circ}.\]

\[Опустим\ перпендикуляр\ O‍_{2}H‍\ \]

\[из\ центра\ O‍_{2}‍\ второй\ \]

\[окружности\ на\ её\ хорду\ BC:\]

\[H - середина\ \text{BC.}\]

\[⊿BO_{2}H = ⊿ABC - по\ катету\ и\ \]

\[противолежащему\ острому\ \]

\[углу:\]

\[AC = \frac{1}{2}BC = BH - по\ условию\ \]

\[задачи;\]

\[\angle BO_{2}H = 90{^\circ} - \angle O_{2}BH = \angle ABC.\]

\[Отсюда:\]

\[O_{2}B = AB;\]

\[\angle AO_{2}B = \angle BAO_{2} = 45{^\circ}.\]

\[Ответ:45{^\circ}.\]

\[\boxed{\mathbf{33.}}\]

\[Дано:\]

\[Решение.\]

\[Поскольку\ окружности\ \]

\[касаются\ внешним\ образом,\ то\ \]

\[расстояние\ O_{1}O_{2}\ между\ их\ \]

\[центрами\ равно\ сумме\ их\ \]

\[радиусов.\ \]

\[Длина\ отрезка\ O_{1}P\ равна\ \]

\[разности\ радиусов,\ а\ \]

\[искомое\ расстояние\ ME\ равно\ \]

\[длине\ отрезка\ PO_{2},\ которую\ \]

\[можно\ найти\ по\ теореме\ \]

\[Пифагора:\ \]

\[PO_{2} = \sqrt{\left( r_{1} + r_{2} \right)^{2} - \left( r_{1} - r_{2} \right)^{2}} =\]

\[= 2\sqrt{r_{1}r_{2}}.\]

\[Возможны\ два\ случая.\]

\[1)\ \]

\[MP = EF = EO_{3} + O_{3}F:\]

\[2\sqrt{r_{1}r_{2}} = 2\sqrt{r_{2}r_{3}} + 2\sqrt{r_{3}r_{1}}\]

\[\sqrt{r_{3}} = \frac{\sqrt{r_{1}r_{2}}}{\sqrt{r_{1}} + \sqrt{r_{2}}} = \frac{6}{5} = 1,2;\]

\[r_{3} = 1,44.\]

\[2)\ \ Аналогично:\]

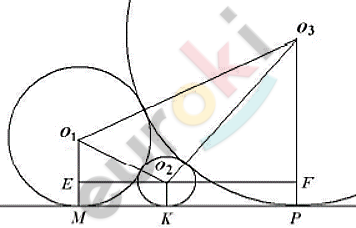
\[2\sqrt{r_{1}r_{3}} = 2\sqrt{r_{1}r_{2}} + 2\sqrt{r_{2}r_{3}}\]

\[\sqrt{r_{3}} = \frac{\sqrt{r_{1}r_{2}}}{\sqrt{r_{1}} - \sqrt{r_{2}}} = 6\]

\[r_{3} = 36.\]

\[Ответ:1,44\ или\ 36.\]

\[\boxed{\mathbf{34.}}\]

\[Дано:\]

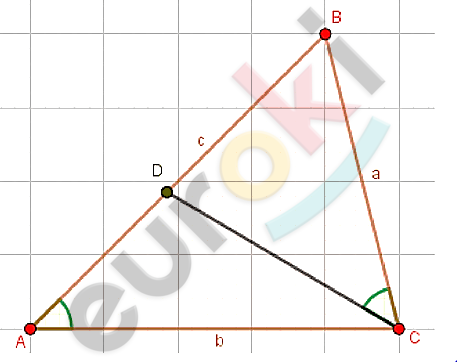
\[Решение.\]

\[⊿BCD\ подобен\ ⊿BAC - по\ двум\ \]

\[углам:\]

\[\angle BCD = \angle BAC - по\ условию;\]

\[\angle ABC - общий.\]

\[Отсюда:\]

\[\frac{\text{BC}}{\text{BA}} = \frac{\text{CD}}{\text{AC}}\]

\[CD = \frac{\text{BC}}{\text{BA}} \cdot AC = \frac{a}{c} \cdot b = \frac{\text{ab}}{c}.\]

\[Ответ:\ \frac{\text{ab}}{c}.\]

\[\boxed{\mathbf{35.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ O - точка\ пересечения\ \]

\[\text{BM\ }и\ \text{KL.}\]

\[Обозначим:\]

\[\frac{\text{BO}}{\text{BM}} = x;\ \ S_{\text{ABC}} = s.\]

\[Получаем:\]

\[S_{\text{BKL}} = \frac{3}{5} \cdot \frac{1}{3}s = \frac{1}{5}s;\]

\[S_{\text{ABM}} = \frac{1}{4}s;\]

\[S_{\text{BCM}} = \frac{3}{4}s;\]

\[S_{\text{BOK}} = \frac{3}{5}x \cdot S_{\text{ABM}} = \frac{3}{20}xs;\]

\[S_{\text{BOL}} = \frac{1}{3}xS_{\text{BCM}} = \frac{1}{4}\text{xs.}\]

\[Так\ как\ \ S_{\text{BKL}} = S_{\text{BOK}} + S_{\text{BOL}}:\]

\[\frac{1}{5} = \frac{3}{20}x + \frac{1}{4}x\ \ \ \ | \cdot 20\]

\[4 = 3x + 5x\]

\[8x = 4\]

\[x = \frac{1}{2}.\]

\[Ответ:\ \ 1\ :2.\]

\[\boxed{\mathbf{36.}}\]

\[Дано:\]

\[Решение.\]

\[Указанная\ прямая\ отсекает\ от\ \]

\[данного\ треугольника\ \]

\[подобный\ ему\ треугольник,\ \]

\[площадь\ которого\ относится\ к\ \]

\[площади\ данного\ \]

\[как\ \ 1\ :\ 2.\ \ \]

\[Поэтому\ коэффициент\ подобия\ \]

\[равен:\]

\[k = \frac{1}{\sqrt{2}}.\]

\[Следовательно,\ длина\ искомого\ \]

\[отрезка:\]

\[\frac{1}{\sqrt{2}} \cdot 36 = 18\sqrt{2}.\]

\[\boxed{\mathbf{37.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ K\ ,\ L\ ,\ M\ и\ N\ —\ середины\ \]

\[сторон\ соответственно\ \]

\[AB\ ,\ BC\ ,\ CD\ и\ AD\ \]

\[данного\ выпуклого\ \]

\[четырёхугольника\ ABCD.\ \]

\[Поскольку\ KL\ и\ MN\ —\ средние\ \]

\[линии\ треугольников\ ABC\ и\ \]

\[ADC:\]

\[KL\ \parallel MN\ и\ KL\ = \ MN.\]

\[Значит,\ четырёхугольник\ \]

\[KLMN\ —\ параллелограмм;\]

\[его\ диагонали\ KM\ и\ LN\ равны:\]

\[KLMN\ —\ прямоугольник.\ \]

\[Стороны\ прямоугольника\ \]

\[KLMN\ параллельны\ \]

\[диагоналям\ AC\ и\ BD\ \]

\[четырёхугольника\ ABCD,\ \]

\[поэтому\ диагонали\ \]

\[четырёхугольника\ ABCD\ \]

\[взаимно\ перпендикулярны.\ \]

\[Следовательно:\]

\[S_{\text{ABCD}} = \frac{1}{2}AC \cdot BD = \frac{1}{2} \cdot 8 \cdot 12 =\]

\[= 48.\]

\[Ответ:48.\]

\[\boxed{\mathbf{38.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ ⊿ABD\ —\ равнобедренный,\ \]

\[т.к.\ его\ биссектриса\ BF\ \]

\[является\ высотой:\]

\[AF = FD;\]

\[S_{\text{AFE}} = S_{\text{DFE}} = 5.\]

\[2)\ BC = 2BD = 2AB;по\ \]

\[свойству\ биссектрисы\ \]

\[треугольника:\]

\[\frac{\text{EC}}{\text{AE}} = \frac{\text{BC}}{\text{AB}} = 2.\]

\[Отсюда:\]

\[S_{\text{DEC}} = 2S_{\text{ADE}} = 4S_{\text{DEF}} = 20;\]

\[S_{\text{ADC}} = 30;\]

\[S_{\text{ABC}} = 2S_{\text{ADC}} = 60.\]

\[Ответ:60.\]

\[\boxed{\mathbf{39.}}\]

\[Дано:\]

\[Решение.\]

\[Пусть\ O - точка\ пересечения\ \]

\[продолжения\ боковых\ сторон\ \]

\[\text{AB\ }и\ DC;\]

\[S - площадь\ треугольника\ \]

\[BOC;\]

\[\frac{S_{\text{BMNC}}}{S_{\text{MADN}}} = \frac{2}{3};\]

\[MN = x - искомый\ отрезок.\]

\[Тогда:\]

\[S_{\text{MNO}} - S = \frac{2}{3}\left( S_{\text{AOD}} - S_{\text{MNO}} \right)\]

\[\frac{x^{2}}{a^{2}} \cdot S - S = \frac{2}{3}\left( \frac{b^{2}}{a^{2}} \cdot S - \frac{x^{2}}{a^{2}} \cdot S \right)\]

\[x^{2} = \frac{3a^{2} + 2b^{2}}{2}\]

\[x = \sqrt{\frac{3a^{2} + 2b^{2}}{2}}.\]

\[Если\ \ \frac{S_{\text{BMNC}}}{S_{\text{MADN}}} = \frac{3}{2}:\]

\[x = \sqrt{\frac{2a^{2} + 3b^{2}}{5}}.\]

\[\boxed{\mathbf{40.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ Проведем\ BH\bot AC\ на\ \]

\[продолжение\ стороны\ \text{AC.}\]

\[S_{\text{ABC}} = \frac{1}{2}AC \cdot BH.\]

\[2)\ ⊿AMC - вписан\ в\ \]

\[окружность\ на\ диаметре:\]

\[\angle AMC = 90{^\circ}.\]

\[3)\ AM - медиана\ и\ высота\ \]

\[⊿BAC:\]

\[⊿BAC - равнобедренный;\]

\[AB = AC = 1.\]

\[4)\ Получаем:\]

\[AD = \frac{2}{3}AB = \frac{2}{3} \cdot 1 = \frac{2}{3}.\]

\[5)\ ⊿ADC - вписан\ в\ \]

\[окружность\ на\ диаметре:\]

\[\angle ADC = 90{^\circ};\]

\[AD = \frac{2}{3};\]

\[AC = 1.\]

\[Отсюда:\]

\[CD = \sqrt{AC^{2} - AD^{2}} = \sqrt{1 - \frac{4}{9}} =\]

\[= \sqrt{\frac{5}{9}} = \frac{\sqrt{5}}{3}.\]

\[6)\ ⊿BHA = ⊿CDA - по\ \]

\[гипотенузе\ и\ острому\ углу:\]

\[\angle BAH = \angle CAD -\]

\[вертикальные;\]

\[AB = AC.\]

\[Отсюда:\]

\[BH = CD = \frac{\sqrt{5}}{3}.\]

\[Ответ:\ \frac{\sqrt{5}}{3}.\]

\[\boxed{\mathbf{41.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ Проведем\ BE \parallel CD.\]

\[2)\ BC \parallel ED;\ \ BE \parallel CD:\]

\[BCDE - параллелограмм.\]

\[3)\ Проведем\ BH\bot AD.\]

\[4)\ В\ треугольнике\ ABE:\]

\[AB = 3;\]

\[BE = CD = 4;\]

\[AE = AD - BC = 5.\]

\[5)\ ⊿ABE - прямоугольный:\]

\[5 = \sqrt{3^{2} + 4^{2}};\]

\[AE = \sqrt{AB^{2} + BE^{2}}.\]

\[6)\ S_{\text{ABE}} = \frac{1}{2}AB \cdot BE = \frac{1}{2}AE \cdot BH\]

\[BH = \frac{AB \cdot BE}{\text{AE}} = \frac{3 \cdot 4}{5} = 2,4.\]

\[7)\ S_{\text{ABCD}} = \frac{AD + BC}{2} \cdot BH =\]

\[= \frac{18 + 13}{2} \cdot \frac{12}{5} = \frac{186}{5} = 37,2.\]

\[Ответ:37,2.\]

\[\boxed{\mathbf{42.}}\]

\[Дано:\]

\[Решение.\]

\[1)\ В\ треугольнике\ OCM:\]

\[\angle OMC = 90{^\circ};\]

\[OM = R;\]

\[OC = OB + BC = 3R.\]

\[Отсюда:\]

\[CM = \sqrt{OC^{2} - OM^{2}} =\]

\[= \sqrt{(3R)^{2} - R^{2}} = \sqrt{8R^{2}} = 2\sqrt{2}\text{R.}\]

\[2)\sin{\angle OCM} = \frac{\text{OM}}{\text{OC}} = \frac{R}{3R} = \frac{1}{3}.\]

\[3)\ S_{\text{ACM}} =\]

\[= \frac{1}{2}AC \cdot CM \cdot \sin{\angle OCM} =\]

\[= \frac{1}{2} \cdot 4R \cdot 2\sqrt{2}R \cdot \frac{1}{3} = \frac{4\sqrt{2}}{3}R^{2}.\]

\[Ответ:\ \frac{4\sqrt{2}}{3}R^{2}.\]

\[\boxed{\mathbf{43.}}\]

\[Дано:\]

\[Решение.\]

\[На\ продолжении\ медианы\ AM\ \]

\[за\ точку\ M\ отложим\ отрезок\ \]

\[MK,\ равный\ AM.\ \]

\[Тогда\ ABKC\ –\ параллелограмм.\ \]

\[Обозначим\ \ AB\ = \ c.\ \ \]

\[Треугольники\ AOD\ и\ KOC\ \]

\[подобны\ (по\ двум\ углам):\]

\[AD = KC \cdot \frac{\text{OD}}{\text{OC}} = AB \cdot \frac{\text{OD}}{\text{OC}} =\]

\[= AB \cdot \frac{5}{9} = 3a \cdot \frac{5}{9} = \frac{5}{3}a;\]

\[BD = AB - AD = 3a - \frac{5a}{3} = \frac{4a}{3}.\]

\[По\ свойству\ биссектрисы\ \]

\[треугольника:\]

\[\frac{\text{BC}}{\text{AC}} = \frac{\text{BD}}{\text{AD}} = \frac{4a}{3}\ :\frac{5a}{3} = \frac{4}{5}.\]

\[Пусть\ AB = 3a;\ \ AC = 5a;\ \ \]

\[BC = 4a.\]

\[По\ теореме\ Пифагора:\]

\[BC^{2} + BD^{2} = CD^{2}\]

\[16a^{2} + \left( \frac{4a}{3} \right)^{2} = 14^{2}\]

\[a^{2} = \frac{49 \cdot 9}{4 \cdot 10}.\]

\[Получаем:\]

\[S_{\text{ABC}} = \frac{1}{2}BC \cdot AB = \frac{1}{2} \cdot 4a \cdot 3a =\]

\[= 6a^{2} = 6 \cdot \frac{49 \cdot 9}{4 \cdot 10} = \frac{1323}{20}.\]

\[Ответ:\ \frac{1323}{20}.\]