Решебник по геометрии 10 класс Атанасян ФГОС 868

\[\boxed{\mathbf{868.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[y = \frac{k}{x};\]

\[k > 0.\]

\[Найти:\]

\[e;\ \]

\[x = \frac{a^{2}}{c}.\]

\[Решение.\]

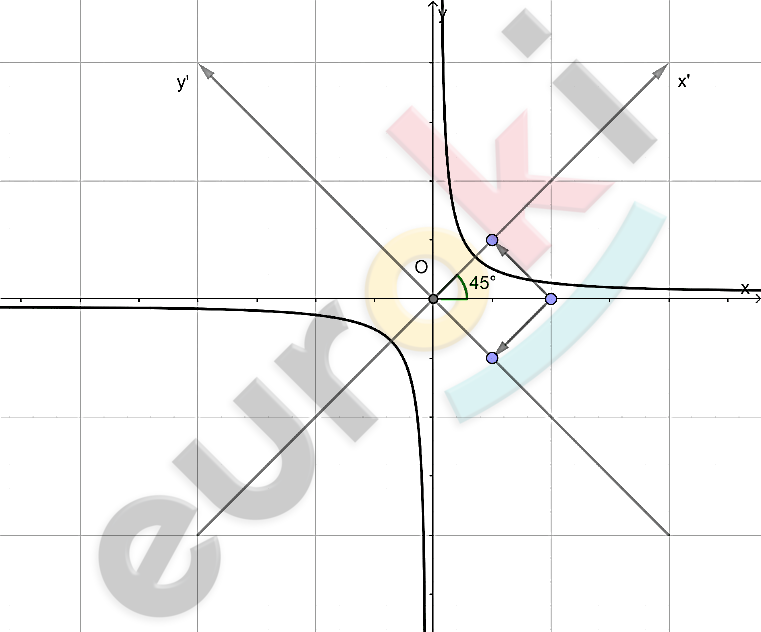
\[1)\ Зададим\ ось\ координат\ \]

\[Ox^{'}y^{'}поворотом\ осей\ Ox\ и\ \text{Oy\ }\]

\[на\ 45{^\circ}\ против\ часовой\ стрелки:\]

\[x^{'} = \sin{45{^\circ}} \bullet (x + y) =\]

\[= \frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}y;\]

\[y^{'} = \sin{45{^\circ}} \bullet (x - y) =\]

\[= \frac{1}{\sqrt{2}}x - \frac{1}{\sqrt{2}}\text{y.}\]

\[2)\ Значит:\ \]

\[x = \sqrt{2}\left( x^{'} + y^{'} \right);\text{\ \ }\]

\[y = \sqrt{2}\left( x^{'} - y^{'} \right).\]

\[3)\ Уравнение\ гиперболы\ в\ \]

\[координатах\ Ox^{'}y^{'}:\]

\[y = \frac{k}{x}\text{\ \ }\]

\[k = xy = 2\left( x^{'2} - y^{'2} \right)\]

\[\frac{x^{'2}}{\frac{k}{2}} - \frac{y^{'2}}{\frac{k}{2}} = 1\ \]

\[a^{2} = \frac{k}{2};\ \]

\[b^{2} = \ c^{2} - a^{2} = \frac{k}{2};\ \]

\[c^{2} = k.\]

\[4)\ Эксцентриситет\ равен:\ \]

\[e = \frac{c}{a} = \frac{\sqrt{k}}{\sqrt{\frac{k}{2}}} = \sqrt{2}.\]

\[5)\ Уравнения\ директрис:\]

\[x^{'} = \frac{a^{2}}{c} = \frac{k}{2\sqrt{k}} = \frac{\sqrt{k}}{2};\ \ \text{\ \ }\]

\[x^{'} = \frac{1}{\sqrt{2}}x + \frac{1}{\sqrt{2}}\text{y.}\]

\[Отсюда:\ \]

\[\frac{y}{\sqrt{2}} + \frac{x}{\sqrt{2}} - \frac{\sqrt{k}}{2} = 0\]

\[y + x - \sqrt{\frac{k}{2}} = 0;\]

\[y + x + \sqrt{\frac{k}{2}} = 0.\]

\[\mathbf{Ответ}:\ \ e = \sqrt{2};\ \ \]

\[y + x - \sqrt{\frac{k}{2}} = 0;\ \ y + x + \sqrt{\frac{k}{2}} = 0.\]