Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 846
846
\[\boxed{\mathbf{846.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\ \ \]
\[ABCD - четырехугольник;\ \ \]
\[AB = b;\ \ BC = c;\ \ CD = d;\ \ \]
\[DA = a;\]
\[p - полуперимтер;\ \ \]
\[вневписанные\ окружности\ \]
\[\left( O_{1};r_{a} \right);\ \ \left( O_{2};r_{c} \right)\text{.\ \ \ }\]
\[Доказать:\ \text{\ \ }\]
\[S_{\text{ABCD}} = r_{a}(p - a) + r_{c}(p - c).\]
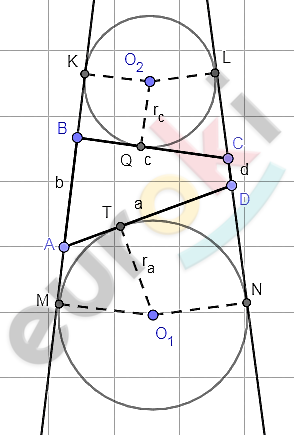
\[Доказательство.\]
\[1)\ Касательные\ из\ одной\ \]
\[точки:\ \]
\[AT = AM,\ \ \ DT = DN,\ \ \ BQ = BK,\ \ \ \]
\[CL = CQ.\]
\[2)\ Пусть\ AT = AM = k;\ \ \]
\[DT = DN = a - k;\ \ \]
\[BQ = BK = l:\]
\[CL = CQ = c - l.\]
\[l + b + l = a - k + d + c - l\ \ \]
\[2k + 2l = (a - b + c + d)\]
\[k + l = \frac{a - b + c + d}{2} = p - b.\]
\[Отсюда:\]
\[KM = k + b + l = p - b + b = p.\]
\[4)\ \ O_{1}M\bot MK\ и\ \ O_{2}K\bot MK:\ \]
\[O_{1}M \parallel O_{2}\text{K.}\]
\[Аналогично:\ \ \ O_{1}N \parallel O_{2}\text{L.}\]
\[Значит:\ \]
\[O_{1}\text{MK}O_{2}\ и\ \ O_{1}O_{2}LN -\]
\[прямоугольные\ трапеции.\]
\[S_{O_{1}\text{MK}O_{2}\text{LN}} = S_{O_{1}\text{MK}O_{2}} + S_{O_{1}O_{2}\text{LN}} =\]
\[= \frac{1}{2}\text{MK}\left( r_{a} + r_{c} \right) + \frac{1}{2}\text{LN}\left( r_{a} + r_{c} \right) =\]
\[= MK\left( r_{a} + r_{c} \right) = p\left( r_{a} + r_{c} \right).\]
\[5)\ S_{O_{1}\text{MADN}} = 2S_{O_{1}\text{AT}} + 2S_{O_{1}\text{TD}} =\]
\[= r_{a}k + r_{a}(a - k) =\]
\[= r_{a}k + r_{a}a - r_{a}k = r_{a}a;\]
\[S_{\text{BK}O_{2}\text{LC}} = 2S_{\text{KBQ}} + 2S_{\text{LCQ}} =\]
\[= r_{c}l + r_{c}(c - l) =\]
\[= r_{c}l + r_{c}c - r_{c}l = r_{c}\text{c.}\]
\[6)\ Таким\ образом:\]
\[S_{\text{ABCD}} =\]
\[= S_{O_{1}\text{MK}O_{2}\text{LN}} - S_{O_{1}\text{MADN}} - S_{\text{BK}O_{2}\text{LC}} =\]
\[= p\left( r_{a} + r_{c} \right) - r_{a}a - r_{c}c =\]
\[= pr_{a} + pr_{c} - r_{a}a - r_{c}c =\]
\[= r_{a}(p - a) + r_{a}(p - c).\]
\[Что\ и\ требовалось\ доказать.\]
