Решебник по геометрии 10 класс Атанасян ФГОС 835

\[\boxed{\mathbf{835.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

\[\text{ABCD} - четырехугольник;\ \ \]

\[в\ закрашенные\ \]

\[четырехугольники\ можно\ \]

\[вписать\ окружность.\]

\[Доказать:\ \ \]

\[в\ \text{ABCD\ }можно\ вписать\ \]

\[окружность.\]

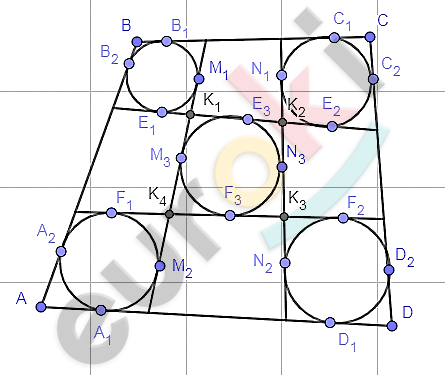
\[Доказательство:\]

\[1)\ Впишем\ окружности\ в\ \]

\[закрашенные\ \]

\[четырехугольники\ и\ отметим\ \]

\[точки\ касания\ ими\ сторон\ \]

\[четырехугольника\ (как\ на\ \]

\[рисунке),\ также\ отметим\ \]

\[пересечения\ данных\ отрезков\ \]

\[точками\ K_{1},K_{2},K_{3},K_{4}.\]

\[2)\ Как\ касательные\ из\ одной\ \]

\[точки:\]

\[BB_{1} = BB_{2};\ \ \]

\[CC_{1} = CC_{2};\ \ \]

\[AA_{2} = AA_{1};\ \ \ \]

\[DD_{1} = DD_{2}.\]

\[Тогда:\]

\[AB + CD - BC - AD = a =\]

\[= A_{2}B_{2} + C_{2}D_{2} - B_{1}C_{1} - A_{1}D_{1}.\]

\[3)\ Как\ общие\ касательные:\]

\[B_{1}C_{1} = E_{1}E_{2},\ \ \ A_{1}D_{1} = F_{1}F_{2},\ \ \ \]

\[A_{2}B_{2} = M_{1}M_{2},\ \ \ C_{2}D_{2} = N_{1}N_{2}.\]

\[a = M_{1}M_{2} + N_{1}N_{2} - E_{1}E_{2} - F_{1}F_{2}.\]

\[4)\ Как\ касательные\ из\ одной\ \]

\[точки:\]

\[K_{1}M_{1} = K_{1}E_{1},\ \ \ K_{2}N_{1} = K_{2}E_{2},\ \ \ \]

\[K_{3}F_{2} = K_{3}N_{2},\ \ \ K_{4}M_{2} = K_{4}F_{1}.\]

\[Тогда:\]

\[a = K_{1}K_{4} + K_{2}K_{3} - K_{1}K_{2} - K_{4}K_{3};\]

\[5)\ Как\ касательные\ из\ одной\ \]

\[точки:\]

\[K_{1}E_{3} = K_{1}M_{3},\ \ \ K_{2}E_{3} = K_{2}N_{3},\ \ \]

\[K_{3}N_{3} = K_{3}F_{3},\ \ \ K_{4}M_{3} = K_{4}F_{3}\text{.\ }\]

\[Тогда:\]

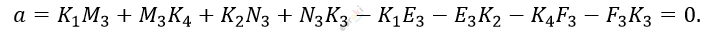
\[6)\ AB + CD - BC - AD = a = 0:\ \]

\[в\ \text{ABCD\ }можно\ вписать\ \]

\[окружность.\]

\[Что\ и\ требовалось\ доказать.\]