Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 831
831
\[\boxed{\mathbf{831.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
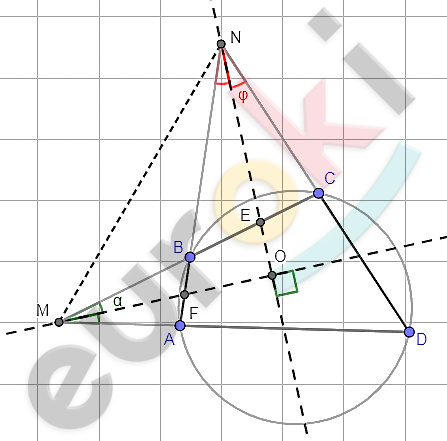
\[Дано:\ \ \]
\[\text{ABCD} - четырехугольник;\ \ \]
\[AB \cap DC = N;\ \ \]
\[CB \cap DA = M;\]
\[\text{NO}\ и\ MO - биссектрисы\ углов\ \]
\[\angle AND\ и\ \angle\text{DMC.}\]
\[Доказать:\ \ \]
\[вокруг\ \text{ABCD\ }можно\ описать\ \]
\[окуружность\ только\ тогда,\]
\[когда\ NO\bot MO.\]
\[Доказательство.\]
\[1)\ Отметим\ точки\ \ E = \text{NO} \cap \text{BC\ \ \ }\]
\[и\ \ \ F = \text{MO} \cap \text{BA.}\]
\[2)\ Пусть\ MO\bot NO.\]
\[Обозначим\ углы\ \angle CMO =\]
\[= \angle OMD = a\ \ и\ \angle ANO =\]
\[= \angle OND = \varphi.\]
\[3)\ В\ \mathrm{\Delta}MEO - прямоугольном:\ \ \ \]
\[\angle MEO = 90{^\circ} - a = \angle NEC\ \]
\[(как\ вертикальные\ углы).\]
\[4)\ В\ \mathrm{\Delta}NEC:\ \ \ \]
\[\angle NCE = 180{^\circ} - \varphi - (90{^\circ} - a) =\]
\[= 90{^\circ} + a - \varphi;\]
\[\angle BCD = 180{^\circ} - (90{^\circ} + a - \varphi) =\]
\[= 90{^\circ} - a + \varphi.\]
\[5)\ В\ \mathrm{\Delta}NFO - прямоугольном:\ \ \]
\[\angle NFO = 90{^\circ} - \varphi = \angle MFA\ \]
\[(как\ вертикальные\ углы).\]
\[6)\ В\ \mathrm{\Delta}MAF:\ \ \ \]
\[\angle MAF = 180{^\circ} - a - (90{^\circ} - \varphi) =\]
\[= 90{^\circ} - a + \varphi;\]
\[\angle BAD = 180{^\circ} - (90{^\circ} - a + \varphi) =\]
\[= 90{^\circ} + a - \varphi.\]
\[7)\ В\ четырехугольнике\ ABCD:\]
\[\angle BAD + \angle BCD =\]
\[= 90{^\circ} + a - \varphi + 90 - a + \varphi =\]
\[= 180{^\circ}.\]
\[Значит,\ около\ него\ можно\ \]
\[описать\ окружность.\]
\[8)\ Обратно,\ пусть\ ABCD -\]
\[вписанный\ четырехугольник.\]
\[В\ \mathrm{\Delta}MNB:\ \ \ \]
\[180{^\circ} - \angle ABC = \angle BMN + \angle MNB;\]
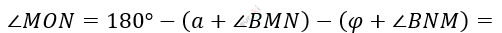
\[= 180{^\circ} - a - \varphi - (\angle BMN + \angle MNB) =\]
\[180{^\circ} - a - \varphi - (180{^\circ} - \angle ABC) =\]
\[= \angle ABC - a - \varphi.\]
\[9)\ \angle ABC = 2\varphi + \angle BCN\ \]
\[\left( как\ внешний\ угол\ у\ \mathrm{\Delta}\text{BNC} \right);\]
\[\angle ABC = 2a + \angle BAM\ \]
\[\left( как\ внешний\ угол\ у\ \mathrm{\Delta}\text{MBA} \right);\]
\[\angle BCN + \angle BAM = 180{^\circ}\ \]
\[Значит:\ \ \]
\[2\angle ABC = 2\varphi + 2a + 180{^\circ}\]
\[\angle ABC = \varphi + a + 90{^\circ}.\]
\[10)\ Таким\ образом:\]
\[\angle MON = \varphi + a + 90{^\circ} - \varphi - a =\]
\[= 90{^\circ}.\]
\[Что\ и\ требовалось\ доказать\text{.\ }\]
