Решебник по геометрии 10 класс Атанасян ФГОС 800

\[\boxed{\mathbf{800.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

\[шары\ O_{1},O_{2},O_{3}O_{4}\ радиуса\ \text{R\ }\]

\[лежат\ на\ плоскости\ a;\ \ \]

\[три\ шара\ попарно\ касаются\ \]

\[друг\ друга,\ а\ четвертый\ \]

\[касается\ только\ двух\ из\ них;\]

\[шары\ O_{5},O_{6}\ меньшего\ \]

\[радиуса\ r,\ касаются\ друг\ друга\ \]

\[и\ касаются\ трех\ больших\ \]

\[шаров.\]

\[Найти:\ \]

\[радиус\ \text{r.}\]

\[Решение.\]

\[1)\ \ Рассмотрим\ проекции\ \]

\[центров\ шаров\ на\ плоскость\ \text{a.}\]

\[2)\ Три\ \ шара\ радиуса\ \text{R\ }попарно\ \]

\[касаются\ друг\ друга,\ \]

\[четвертый\ шар\ касается\ \]

\[только\ двух\ из\ них:\]

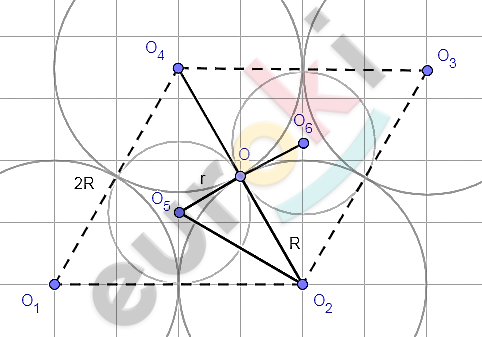
\[\text{\ O}_{1}O_{2}O_{3}O_{4} - ромб\ со\ стороной\ \]

\[2R.\]

\[3)\ Пусть\ шары\ O_{2}O_{4}\ касаются\ \]

\[друг\ друга,\ а\ точка\ O -\]

\[проекция\ точки\ их\ касания\ на\ \]

\[плоскость\ a:\]

\[O_{2}O = OO_{4} = R\]

\[O_{4}O_{2} = 2R.\]

\[Отсюда:\]

\[\mathrm{\Delta}O_{1}O_{2}O_{4} = \mathrm{\Delta}O_{2}O_{3}O_{4} -\]

\[равносторонние.\]

\[4)\ Пусть\ шар\ O_{5}\ касается\ шаров\ \]

\[O_{1},O_{2}\ и\ O_{4},\ а\ шар\ O_{6} - касается\ \]

\[шаров\ O_{2};O_{3}\ и\ O_{4}:\]

\[проекции\ их\ центров\ являются\ \]

\[центрами\ треугольников\]

\[\mathrm{\Delta}O_{1}O_{2}O_{4}\ \ и\ \ \mathrm{\Delta}O_{2}O_{3}O_{4}\ \]

\[(так\ как\ расстояния\ от\ точек\ \]

\[O_{5},O_{6}\ до\ вершин\ этих\ \]

\[треугольников\ равны).\]

\[5)\ O_{3}O\ и\ O_{1}O - медианы\ и\ \]

\[высоты\ этих\ треугольников;\ \]

\[точки\ O_{5}\ и\ O_{6}\ принадлежат\ им:\]

\[O_{5}O_{6}\bot O_{2}O_{4}.\]

\[6)\ \ В\ \mathrm{\Delta}OO_{2}O_{5} - прямоугольном:\]

\[O_{5}O = O_{6}O = r,\ OO_{2} = R,\ O_{2}O_{5} -\]

\[биссектриса\ \angle O_{4}O_{2}O_{1};\]

\[\ \angle OO_{2}O_{5} = 30{^\circ};\]

\[r = R \bullet tg\ 30{^\circ} = R \bullet \frac{\sqrt{3}}{3}.\]

\[Ответ:\ \frac{\sqrt{3}}{3}\text{R.}\]