Решебник по геометрии 10 класс Атанасян ФГОС 797

\[\boxed{\mathbf{797.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

\[сфера\ \text{O.}\text{\ \ }\]

\[Найти:\]

\[ьножество\ всех\ таких\ точек,\ из\ \]

\[которых\ можно\ провести\ к\]

\[данной\ сфере\ три\ попарно\ \]

\[перпендикулярные\ \]

\[касательные\ прямые.\]

\[Решение:\]

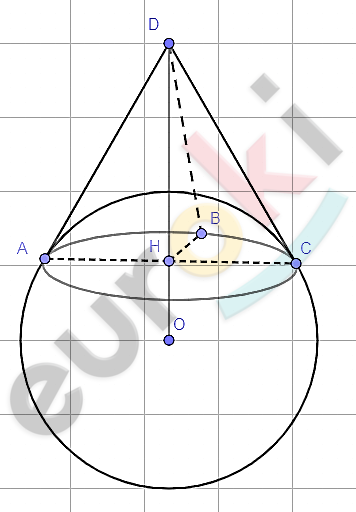
\[1)\ Рассмотрим\ точку\ D - одну\ \]

\[из\ множества\ возможных\ точек.\]

\[Касательные,\ проведенные\ из\ \]

\[этой\ точки:\ \]

\[DA,\ DB\ и\ \text{DC.}\]

\[2)\ \ AO = OB = OC = R_{сф}\ \ и\ \ \]

\[DO - общая\ гипотенуза:\]

\[\mathrm{\Delta}ADO = \mathrm{\Delta}BDO = \mathrm{\Delta}CDO.\]

\[Отсюда:\]

\[DA = DB = DC.\]

\[3)\ \mathrm{\Delta}ADB = \mathrm{\Delta}BDC = \mathrm{\Delta}ADC\ \]

\[(по\ двум\ катетам):\]

\[AB = BC = AC.\]

\[4)\ Опустим\ перпендикуляры\ из\ \]

\[точки\ \text{D\ }на\ плоскость\ ABC:\]

\[\text{DH\ }и\ \text{OH\ }совпадут,\ так\ как\ \]

\[пройдут\ через\ центр\ \]

\[правильного\ \mathrm{\Delta}\text{ABC.}\]

\[5)\ В\ \mathrm{\Delta}ABD - прямоугольном:\ \ \ \ \]

\[AB = \sqrt{AD^{2} + BD^{2}} = \sqrt{2AD^{2}} =\]

\[= DA\sqrt{2}.\]

\[Пусть\ DA = a;\ \ AB = a\sqrt{2};\]

\[AH = BH = r - радиус\ \]

\[описанной\ около\ \mathrm{\Delta}ABC\ \]

\[окружности.\]

\[Получаем:\]

\[AB = AH\sqrt{3};\ \ \]

\[AH = \frac{\text{AB}}{\sqrt{3}} = \frac{a\sqrt{2}}{\sqrt{3}}.\]

\[6)\ \mathrm{\Delta}ODA\sim\mathrm{\Delta}HAD:\ \]

\[\frac{R_{сф}}{\text{DO}} = \frac{\text{AH}}{\text{AD}} = \frac{a\sqrt{\frac{2}{3}}}{a}\]

\[DO = \frac{1}{2}R\sqrt{6}.\]

\[7)\ Следовательно:\]

\[искомое\ множество\ точек -\]

\[это\ сфера,\ центр\ которой\ \]

\[совпадает\ с\ центром\ данной\ \]

\[сферы,\ а\ радиус\ равен\ \frac{1}{2}R\sqrt{6}\text{.\ }\]