Решебник по геометрии 10 класс Атанасян ФГОС 794

\[\boxed{\mathbf{794.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \]

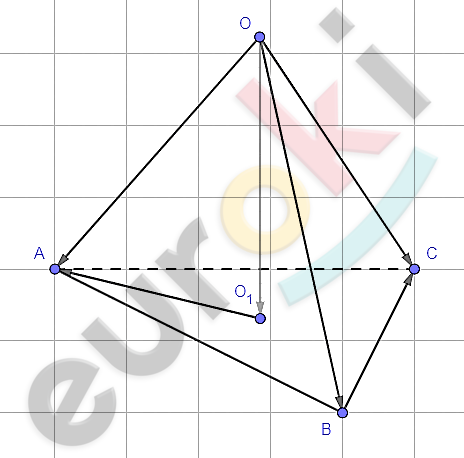
\[OBCD - тетраэдр;\ \ \]

\[AOB\bot BOC\bot COA;\ \]

\[O_{1} - проекция\ точки\ O\ на\ \]

\[плоскость\ ABC.\]

\[Доказать:\ \ \]

\[O_{1} - точка\ пересечения\ высот\ \]

\[\text{ABC}.\]

\[Доказательство.\]

\[1)\ Обозначим\ ребра\ тетраэдра\ \]

\[как\ векторы:\]

\[\overrightarrow{\text{BC}} = \overrightarrow{\text{OC}} - \overrightarrow{\text{OB}};\ \ \]

\[\overrightarrow{O_{1}A} = \overrightarrow{\text{OA}} - \overrightarrow{OO_{1}}.\]

\[2)\ AOB\bot BOC\bot COA:\]

\[\overrightarrow{\text{OA}}\bot\overrightarrow{\text{OC}}\ \ и\ \ \overrightarrow{\text{OA}}\bot\overrightarrow{\text{OB}};\ \ \]

\[OO_{1}\bot ABC;\]

\[\overrightarrow{\text{BC}}\bot\overrightarrow{OO_{1}}.\]

\[Отсюда:\]

\[\overrightarrow{\text{BC}} \bullet \overrightarrow{O_{1}A} =\]

\[= \left( \overrightarrow{\text{OC}} - \overrightarrow{\text{OB}} \right) \bullet \left( \overrightarrow{\text{OA}} - \overrightarrow{OO_{1}} \right) =\]

\[= \overrightarrow{\text{BC}} \bullet \overrightarrow{OO_{1}} = 0.\]

\[Значит:\ \]

\[BC\bot O_{1}\text{A.}\]

\[Аналогично:\ \]

\[O_{1}B\bot AC\ \ и\ \ O_{1}C\bot AB.\]

\[Значит:\ \]

\[точка\ O_{1} - пересечение\ высот\ \]

\[треугольника\ \text{ABC}.\]

\[Что\ и\ требовалось\ доказать.\]