Решебник по геометрии 10 класс Атанасян ФГОС 75

\[\boxed{\mathbf{75.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

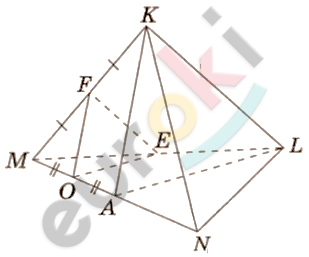
\[\textbf{а)}\ A - середина\ \text{MN.}\]

\[Проведем\ AK\ и\ \text{AL.}\]

\[⊿AKL - сечение.\]

\[\textbf{б)}\ В\ треугольнике\ AMK:\]

\[OF - средняя\ линия;\]

\[OF \parallel AK.\]

\[В\ треугольнике\ MKL:\]

\[EF - средняя\ линия;\]

\[EF \parallel KL.\]

\[По\ теореме\ о\ параллельности\ \]

\[плоскостей:\]

\[OFE \parallel AKL.\]

\[⊿OFE\sim ⊿AKL:\]

\[\angle OFE = \angle AKL;\]

\[OF = \frac{1}{2}AK;\]

\[EF = \frac{1}{2}\text{KL.}\]

\[Получаем:\]

\[\frac{S_{\text{LKA}}}{S_{\text{EOF}}} = \frac{LA^{2}}{EO^{2}} = \frac{LA^{2}}{\frac{1}{4}LA^{2}} = 4.\]

\[S_{\text{LKA}} = 24\ см^{2}:\]

\[S_{\text{EOF}} = 24\ :4 = 6\ см^{2}.\]

\[Ответ:6\ см^{2}.\]