Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 710
710
\[\boxed{\mathbf{710.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\]
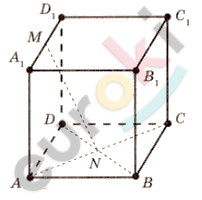
\[AB = a;\]
\[N - точка\ пересечения\ \]
\[диагоналей.\]
\[Решение.\]
\[A(a;0;0);B(a;a;0);C(0;a;0);\]
\[D(0;0;0);\]
\[A_{1}(a;0;a);B_{1}(a;a;a);\]
\[C_{1}(0;a;a);D_{1}(0;0;a).\]
\[M\left( \frac{4a}{5};0;a \right);N\left( \frac{a}{2};\frac{a}{2};0 \right).\]
\[\overrightarrow{\text{DA}}\left\{ a;0;0 \right\};\ \ \overrightarrow{\text{DC}}\left\{ 0;a;0 \right\};\ \ \]
\[\overrightarrow{DD_{1}}\left\{ 0;0;a \right\};\ \ \overrightarrow{\text{MN}}\left\{ - \frac{3a}{10};\frac{a}{2}; - a \right\}.\]
\[\textbf{а)}\ \overrightarrow{DD_{1}}\bot\left( \text{ABCD} \right):\]
\[\sin{\angle\left( \overrightarrow{\text{MN}};\left( \text{ABCD} \right) \right)} =\]
\[= \left| \cos{\angle\left( \overrightarrow{\text{MN}};\overrightarrow{DD_{1}} \right)} \right| =\]
\[= \frac{\left| 0 + 0 - a^{2} \right|}{\sqrt{\frac{9a^{2}}{100} + \frac{{a^{2}}^{\backslash 25}}{4} + {a^{2}}^{\backslash 100}} \cdot \sqrt{a^{2}}} =\]
\[= \frac{a^{2}}{a\sqrt{\frac{134}{100}} \cdot a} = \frac{10}{\sqrt{134}}.\]
\[\textbf{б)}\ \overrightarrow{\text{DA}}\bot\left( DD_{1}C_{1}C \right):\]
\[\sin{\angle\left( \overrightarrow{\text{MN}};\left( DD_{1}C_{1}C \right) \right)} =\]
\[= \left| \cos{\angle\left( \overrightarrow{\text{MN}};\overrightarrow{\text{DA}} \right)} \right| =\]
\[= \frac{\left| - \frac{3a}{10} \cdot a + 0 \right|}{\sqrt{\frac{9a^{2}}{100} + \frac{a^{2}}{4} + a^{2}} \cdot \sqrt{a^{2}}} =\]
\[= \frac{\frac{3a^{2}}{10}}{a^{2}\sqrt{\frac{134}{100}}} = \frac{3}{\sqrt{134}}.\]
\[\textbf{в)}\ \overrightarrow{\text{DC}}\bot\left( AA_{1}D_{1}D \right):\ \]
\[\sin{\angle\left( \overrightarrow{\text{MN}};\left( AA_{1}D_{1}D \right) \right)} =\]
\[= \left| \cos{\angle\left( \overrightarrow{\text{DC}};\overrightarrow{\text{MN}} \right)} \right| =\]
\[= \frac{\left| \frac{a}{2} \cdot a + 0 \right|}{\sqrt{\frac{9a^{2}}{100} + \frac{a^{2}}{4} + a^{2}} \cdot \sqrt{a^{2}}} =\]
\[= \frac{\frac{a^{2}}{2}}{a^{2}\sqrt{\frac{134}{100}}} = \frac{5}{\sqrt{134}}.\]
