Решебник по геометрии 10 класс Атанасян ФГОС 691

\[\boxed{\mathbf{691.}еуроки - ответы\ на\ пятёрку}\]

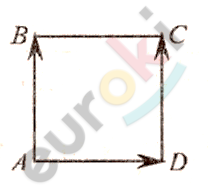
\[A(0;1;2);\ \ B\left( \sqrt{2};1;2 \right);\ \ \]

\[C\left( \sqrt{2};2;1 \right);\ \ D(0;2;1).\]

\[Доказательство.\]

\[1)\ Данный\ четырехугольник\ \]

\[параллелограмм:\]

\[BC = AD;\]

\[BC \parallel AD.\]

\[\overrightarrow{\text{BC}}\left\{ 0;1; - 1 \right\};\ \ \overrightarrow{\text{AD}}\left\{ 0;1; - 1 \right\}:\]

\[\overrightarrow{\text{BC}} = \overrightarrow{\text{AD}}.\]

\[2)\ Этот\ параллелограмм -\]

\[прямоугольник:\]

\[AB\bot AD.\]

\[\overrightarrow{\text{AB}}\left\{ \sqrt{2};0;0 \right\};\ \ \overrightarrow{\text{AD}}\left\{ 0;1; - 1 \right\}:\]

\[\overrightarrow{\text{AB}} \cdot \overrightarrow{\text{AD}} = \sqrt{2} \cdot 0 + 0 \cdot 1 - 0 \cdot 1 =\]

\[= 0.\]

\[3)\ Этот\ параллелограмм\ -\]

\[ромб:\]

\[BD\bot AC.\]

\[\overrightarrow{\text{BD}}\left\{ - \sqrt{2};1; - 1 \right\};\ \ \overrightarrow{\text{AC}}\left\{ \sqrt{2};1; - 1 \right\}:\]

\[\overrightarrow{\text{AC}} \cdot \overrightarrow{\text{BD}} =\]

\[= - \sqrt{2} \cdot \sqrt{2} + 1 \cdot 1 + 1 \cdot 1 = 0.\]

\[Следовательно:\]

\[ABCD - квадрат.\]

\[Что\ и\ требовалось\ доказать.\]