Решебник по геометрии 10 класс Атанасян ФГОС 64

\[\boxed{\mathbf{64.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

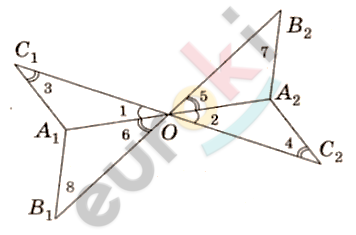
\[Доказательство.\]

\[1)\ Прямые\ A_{1}A_{2}\ и\ C_{1}C_{2}\ задают\ \]

\[плоскость\ A_{1}C_{1}C_{2}.\]

\[По\ свойству\ параллельности\ \]

\[плоскостей:\]

\[A_{1}C_{1} \parallel A_{2}C_{2}.\]

\[Аналогично:\]

\[A_{1}B_{1} \parallel A_{2}B_{2};\]

\[B_{1}C_{1} \parallel B_{2}C_{2}.\]

\[2)\ ⊿OA_{2}C_{1}\sim ⊿OA_{2}C_{2} - по\ двум\ \]

\[углам:\]

\[\angle 1 = \angle 2;\]

\[\angle 3 = \angle 4.\]

\[Из\ подобия\ треугольников:\]

\[\frac{A_{1}C_{1}}{A_{2}C_{2}} = \frac{OA_{1}}{OA_{2}} = \frac{OC_{1}}{OC_{2}}.\]

\[3)\ ⊿OA_{1}B_{1}\sim ⊿OA_{2}B_{2}:\]

\[\frac{A_{1}B_{1}}{A_{2}B_{2}} = \frac{OA_{1}}{OA_{2}} = \frac{OB_{1}}{OB_{2}}.\]

\[4)\ ⊿OB_{1}C_{1}\sim ⊿OB_{2}C_{2}:\]

\[\frac{B_{1}C_{1}}{B_{2}C_{2}} = \frac{OB_{1}}{OB_{2}} = \frac{OC_{1}}{OC_{2}}.\]

\[5)\ Из\ всех\ соотношений\ \]

\[получаем:\]

\[\frac{A_{1}C_{1}}{A_{2}C_{2}} = \frac{A_{1}B_{1}}{A_{2}B_{2}} = \frac{B_{1}C_{1}}{B_{2}C_{2}}.\]

\[Следовательно:\]

\[⊿A_{1}B_{1}C_{1}\sim ⊿A_{2}B_{2}C_{2}.\]

\[Что\ и\ требовалось\ доказать.\]