Решебник по геометрии 10 класс Атанасян ФГОС 601

\[\boxed{\mathbf{601.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

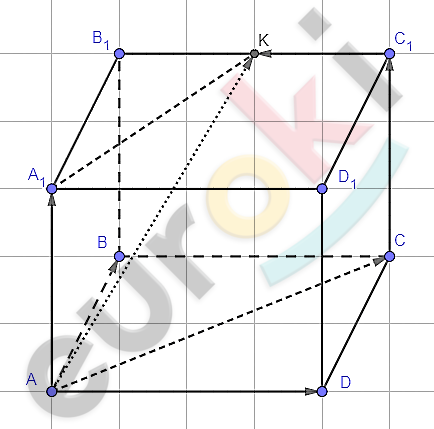
\[\text{ABCD}A_{1}B_{1}C_{1}D_{1} - куб;\]

\[B_{1}K = KC_{1}.\]

\[Разложить:\ \ \]

\[вектор\ \overrightarrow{\text{AK}}\ по\ векторам\ \]

\[\overrightarrow{a} = \overrightarrow{\text{AB}};\ \overrightarrow{b} = \ \overrightarrow{\text{AD}};\ \ \overrightarrow{c} = \overrightarrow{AA_{1}}.\]

\[Найти:\]

\[длину\ \overrightarrow{\text{AK}},\ если\ ребро\ куба\ \]

\[равно\ \text{m.}\]

\[Решение.\]

\[1)\ По\ правилу\ \]

\[параллелограмма:\]

\[\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{AD}} = \overrightarrow{a} + \overrightarrow{b}.\]

\[2)\ \overrightarrow{\text{AK}} = \overrightarrow{\text{AC}} + \overrightarrow{CC_{1}} + \overrightarrow{C_{1}K};\ \]

\[\overrightarrow{CC_{1}} = \overrightarrow{AA_{1}} = \overrightarrow{c};\ \ \]

\[\overrightarrow{C_{1}K} = - \frac{1}{2}\overrightarrow{\text{AD}} = - \frac{1}{2}\overrightarrow{b}.\]

\[Отсюда:\ \]

\[\overrightarrow{\text{AK}} = \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} - \frac{1}{2}\overrightarrow{b} =\]

\[= \overrightarrow{a} - \frac{1}{2}\overrightarrow{b} + \overrightarrow{c}.\]

\[3)\ \mathrm{\Delta}AA_{1}K - прямоугольный:\ \ \]

\[AA_{1} = m;\ \ \]

\[A_{1}K = \sqrt{m^{2} + \left( \frac{1}{2}m^{2} \right)} = \sqrt{\frac{5}{4}m^{2}}.\]

\[Следовательно:\]

\[AK = \sqrt{AA_{1}^{2} + A_{1}K^{2}} =\]

\[= \sqrt{m^{2} + \frac{5}{4}m^{2}} = \sqrt{\frac{9}{4}m^{2}} = \frac{3}{2}\text{m.}\]

\[Ответ:\ \ \overrightarrow{\text{AK}} = \overrightarrow{a} + \frac{1}{2}\overrightarrow{b} + \overrightarrow{c};\ \ \]

\[|\overrightarrow{\text{AK}}| = \frac{3}{2}\text{m.}\]