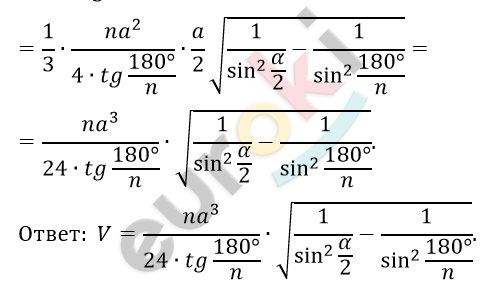Решебник по геометрии 10 класс Атанасян ФГОС 532

\[\boxed{\mathbf{532.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[A_{1}A_{2}A_{3}M - правильная\ \]

\[пирамида;\]

\[MH - высота;\]

\[MH_{1} - апофема;\]

\[A_{1}A_{2} = a;\]

\[\angle A_{1}MA_{2} = \alpha.\]

\[Найти:\]

\[\text{V.}\]

\[Решение.\]

\[1)\ S_{осн} = \frac{na^{2}}{4\ tg\frac{180{^\circ}}{n}}.\]

\[2)\ A_{1}H = R = \frac{a}{2 \bullet \sin\frac{180{^\circ}}{n}}.\]

\[3)\ По\ теореме\ синусов\ в\ \]

\[\mathrm{\Delta}MA_{1}A_{2}:\]

\[\frac{A_{1}M}{\sin\left( 90{^\circ} - \frac{\alpha}{2} \right)} = \frac{a}{\sin\alpha}\]

\[A_{1}M = \frac{a \bullet \sin\left( 90{^\circ} - \frac{\alpha}{2} \right)}{\sin\alpha} =\]

\[= \frac{a \bullet \cos\frac{\alpha}{2}}{2 \bullet \sin{\frac{\alpha}{2} \bullet \cos\frac{\alpha}{2}}} = \frac{a}{2\sin\frac{\alpha}{2}}.\]

\[4)\ \mathrm{\Delta}MA_{1}H - прямоугольный:\]

\[MH = \sqrt{A_{1}M^{2} - A_{1}H^{2}} =\]

\[= \sqrt{\frac{a^{2}}{4\sin^{2}\frac{\alpha}{2}} - \frac{a^{2}}{4 \bullet \sin^{2}\frac{180{^\circ}}{n}}} =\]

\[= \frac{\alpha}{2}\sqrt{\frac{1}{\sin^{2}\frac{\alpha}{2}} - \frac{1}{\sin^{2}\frac{180{^\circ}}{n}}}.\]

\[5)\ V = \frac{1}{3} \bullet S_{осн} \bullet h =\]