Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 531
531
\[\boxed{\mathbf{531.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\]
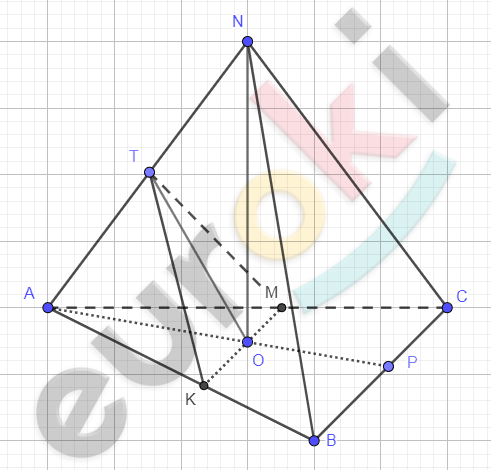
\[ABCN - правильная\ пирамида;\]
\[\angle KTM = \varphi;\]
\[NO - высота\ h.\]
\[Найти:\]
\[\text{V.}\]
\[Решение.\]
\[1)\ Из\ точки\ \text{N\ }опустим\ высоту\ \]
\[NO\bot ABC;\ построим\ через\ \]
\[точку\ \text{O\ }отрезок\ KM \parallel BC.\]
\[2)\ Построим\ пераендикуляр\ \]
\[OT\bot AN.\]
\[3)\ OT \in TKM\ и\ OT\bot AN:\]
\[TKM\bot AN.\]
\[Отсюда:\ \]
\[\angle KTM = 2\varphi;\]
\[\angle KTO = \varphi.\]
\[4)\ В\ \mathrm{\Delta}ONT:\ \ \]
\[HT = h \bullet \sin{\angle BNA};\]
\[KO = OM.\]
\[В\ \mathrm{\Delta}TOK:\ \]
\[\frac{\text{MK}}{h \bullet \sin{\angle BNA}} = tg\ \varphi.\]
\[5)\ \mathrm{\Delta}ABC - правильный:\ \ \]
\[OP = r - радиус\ вписанной\ \]
\[окружности;\]
\[AP - медиана\ и\ высота;\]
\[CP = BP = \frac{1}{2}\text{BC.}\]
\[6)\ \mathrm{\Delta}ACP\ и\ \mathrm{\Delta}AOM\ подобны\ по\ \]
\[трем\ углам\ (OM \parallel BC):\]
\[\frac{\text{OM}}{\text{AO}} = \frac{\text{PC}}{AO + OP}\ \]
\[OM = \frac{PC \bullet AO}{2 \bullet (AO + OP)};\]
\[AO = R = \frac{\text{BC}\sqrt{3}}{3};\]
\[AO + OP = AP;\]
\[AP = AC \bullet \sin{60{^\circ}} =\]
\[= BC \bullet \sin{60{^\circ}} = \frac{\text{BC}\sqrt{3}}{2};\]
\[OM = \frac{BC \bullet BC}{\sqrt{3} \bullet 2 \bullet BC \bullet \frac{\sqrt{3}}{2}} = \frac{\text{BC}}{3};\ \ \]
\[\ OM = OK;\]
\[\text{tg\ }\varphi = \frac{\text{BC}}{3 \bullet h \bullet \sin{\angle BNA}}.\]
\[7)\ \mathrm{\Delta}NOA - прямоугольный:\]
\[\frac{\text{AO}}{h} = tg\ \angle BNA;\ \]
\[\ \frac{\text{BC}}{\sqrt{3}h} = tg\ \angle BNA;\]
\[BC = h\sqrt{3} \bullet tg\ \angle BNA;\]
\[\text{tg\ }\varphi = \frac{h\sqrt{3} \bullet tg\ \angle BNA}{3h \bullet \sin{\angle BNA}};\]
\[\text{tg\ }\varphi =\]
\[= \frac{\sqrt{3}}{3} \bullet \frac{\sin{\angle BNA}}{\sin{\angle BNA} \bullet \cos{\angle BNA}};\]
\[3\cos{\angle BNA} \bullet tg\ \varphi = \sqrt{3}\ \]
\[\cos{\angle BNA =}\frac{\sqrt{3}}{3 \bullet tg\ \varphi};\]
\[AN = \frac{h}{\cos{\angle BNA}} = \frac{h \bullet 3\ tg\ \varphi}{\sqrt{3}} =\]
\[= h\sqrt{3} \bullet tg\ \varphi.\]
\[7)\ \mathrm{\Delta}ANO - прямоугольный:\]
\[AO = \sqrt{AN^{2} - h^{2}} =\]
\[= \sqrt{3h^{2} \bullet tg^{2}\varphi - h^{2}} =\]
\[= h\sqrt{3\ tg^{2}\varphi - 1}.\]
\[8)\ В\ \mathrm{\Delta}ABC:\]
\[AO = \frac{\text{BC}\sqrt{3}}{3}\]
\[BC = \frac{3\ OA}{\sqrt{3}} = \sqrt{3}\text{OA}\]
\[BC = \sqrt{3} \bullet h\sqrt{3\ tg^{2}\ \varphi - 1}.\]
\[9)\ V = \frac{1}{3} \bullet S_{осн}h =\]
\[= \frac{1}{3} \bullet \frac{BC^{2}\sqrt{3}}{4} \bullet h =\]
\[= \frac{1}{3} \bullet \frac{3\sqrt{3}}{4} \bullet \left( 3\ tg^{2}\varphi - 1 \right)h =\]
\[= \frac{h^{3}\sqrt{3}}{4} \bullet \left( 3\ tg^{2}\varphi - 1 \right).\]
\[\mathbf{Отв}ет:\ \ V = \frac{h^{3}\sqrt{3}}{4} \bullet \left( 3\ tg^{2}\varphi - 1 \right).\]
