Решебник по геометрии 10 класс Атанасян ФГОС 384

\[\boxed{\mathbf{384.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

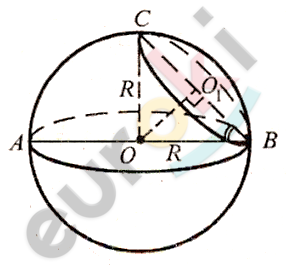
\[Найти:\]

\[\text{L.}\]

\[Решение.\]

\[Проведем\ OO_{1}\bot плоскости\ \]

\[сечения.\]

\[Соединим\ O_{1}\ с\ точками\ \text{B\ }и\ \text{C.}\]

\[C - продолжение\ отрезка\ BO_{1}\ \]

\[до\ пересечения\ его\ со\ сферой.\]

\[⊿\text{COB} - равнобедренный;\ \ \]

\[OO_{1}\bot CB:\]

\[OO_{1} - медиана,\ высота\ и\ \]

\[биссектриса;\]

\[CO_{1} = O_{1}\text{B.}\]

\[O_{1} - центр\ окружности,\ так\ \]

\[как\ равноудалена\ от\ точек\ \]

\[\text{C\ }и\ B,\ лежащих\ на\ окружности,\ \]

\[по\ которой\ сечение\ пересекает\ \]

\[сферу.\]

\[\angle OBO_{1} = \alpha.\]

\[Пусть\ O_{1}B = r.\]

\[\textbf{а)}\ R = 2\ см;\alpha = 30{^\circ}.\]

\[В\ треугольнике\ OO_{1}B:\]

\[O_{1}B = r = R \cdot \cos{30{^\circ}} = \frac{R\sqrt{3}}{2}.\]

\[L = 2\pi r = \frac{2\pi R\sqrt{3}}{2} = \pi R\sqrt{3} =\]

\[= 2\pi\sqrt{3}\ см.\]

\[\textbf{б)}\ R = 5\ м;\ \ \alpha = 45{^\circ}.\]

\[r = R \cdot \cos{45{^\circ}} = \frac{R\sqrt{2}}{2};\]

\[L = 2\pi r = 2\pi \cdot \frac{R\sqrt{2}}{2} = \pi\sqrt{2}R =\]

\[= 5\pi\sqrt{2}\ (м).\]

\[Ответ:а)\ 2\sqrt{3}\pi\ см;б)\ 5\pi\sqrt{2}\ м.\]