Решебник по геометрии 10 класс Атанасян ФГОС 380

\[\boxed{\mathbf{380.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[сфера;\]

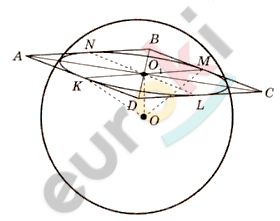
\[O - центр\ сферы;\]

\[ABCD - ромб;\]

\[R = 10\ см;\]

\[DB = 15\ см;\]

\[AC = 20\ см.\]

\[Найти:\]

\[OO_{1}.\]

\[Решение.\]

\[По\ теореме\ о\ трех\ \]

\[перпендикулярах:\]

\[O_{1}L\bot DC;\ \ O_{1}M\bot BC;\ \ \]

\[O_{1}N\bot AB;\ \ O_{1}K\bot AD.\]

\[⊿OO_{1}L = ⊿OO_{1}N = ⊿OO_{1}K =\]

\[= ⊿OO_{1}\text{M\ }(прямоугольные):\]

\[OO_{1} - общий\ катет;\]

\[OK = OL = ON = OM = R.\]

\[Следовательно:\]

\[O_{1} - центр\ окружности,\ \]

\[вписанной\ в\ ромб\ \text{ABCD.}\]

\[По\ теореме\ Пифагора\ \]

\[\left( из\ ⊿OO_{1}L \right):\]

\[OO_{1} = \sqrt{OL^{2} - O_{1}L^{2}} = \sqrt{R^{2} - r^{2}}.\]

\[O_{1}C = \frac{1}{2}AC = 10\ см;\]

\[O_{1}D = \frac{1}{2}BD = \frac{15}{2}\ см;\]

\[CD = \sqrt{O_{1}C^{2} + O_{1}D^{2}} =\]

\[= \sqrt{10^{2} + \left( \frac{15}{2} \right)^{2}} = \frac{25}{2}\ см.\]

\[S_{O_{1}\text{CD}} = \frac{1}{2}CD \cdot O_{1}L = \frac{1}{2} \cdot \frac{25}{2} \cdot r =\]

\[= \frac{25r}{4};\]

\[S_{O_{1}\text{CD}} = \frac{1}{4}S_{\text{ABCD}} = \frac{1}{4} \cdot \frac{1}{2}AC \cdot BD =\]

\[= \frac{1}{8} \cdot 20 \cdot 15 = \frac{75}{2};\]

\[\frac{25r}{4} = \frac{75}{2}\]

\[r = \frac{75 \cdot 4}{2 \cdot 25} = 6\ см.\]

\[OO_{1} = \sqrt{10^{2} - 6^{2}} = \sqrt{64} = 8\ см.\]

\[Ответ:8\ см.\]