Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 342
342
\[\boxed{\mathbf{342.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\]
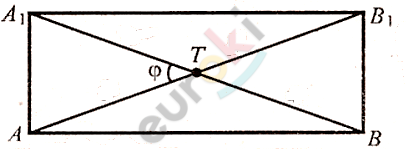
\[развертка\ боковой\ \]
\[поверхности\ цилиндра;\]
\[\angle между\ диагоналями = \varphi;\]
\[диагональ = d.\]
\[Найти:\]
\[S_{бок};\ \ S_{полн}.\]
\[Решение.\]
\[S_{бок} = 2\pi Rh;\]
\[S_{полн} = 2\pi R(h + R).\]
\[1)\ AB = 2\pi R;\]
\[R = \frac{\text{AB}}{2\pi};\]
\[h = AA_{1}.\]
\[2)\ Диагонали\ прямоугольника\ \]
\[равны\ и\ точкой\ \text{T\ }делятся\ \]
\[пополам.\]
\[По\ теореме\ косинусов\ \]
\[\left( в\ ⊿ATA_{1} \right):\]
\[AA_{1}^{2} =\]
\[= \left( \frac{d}{2} \right)^{2} + \left( \frac{d}{2} \right)^{2} - 2 \cdot \frac{d}{2} \cdot \frac{d}{2} \cdot \cos\varphi =\]
\[= \frac{2d^{2}}{4} - \frac{2d^{2}}{4} \cdot \cos\varphi =\]
\[= \frac{d^{2}}{2}\left( 1 - \cos\varphi \right) =\]
\[= \frac{d^{2}}{2} \cdot 2\sin^{2}\frac{\varphi}{2} = d^{2}\sin^{2}\frac{\varphi}{2}.\]
\[AA_{1} = \sqrt{d^{2}\sin^{2}\frac{\varphi}{2}} = d\sin\frac{\varphi}{2};\ \ \]
\[AA_{1} = h.\]
\[По\ теореме\ косинусов\ \]
\[(в\ ⊿ATB):\]
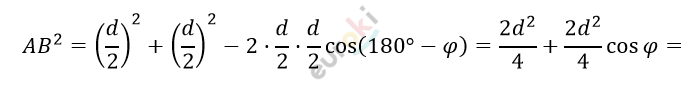
\[= \frac{d^{2}}{2}\left( 1 + \cos\varphi \right) =\]
\[= \frac{d^{2}}{2} \cdot 2\cos^{2}\frac{\varphi}{2} = d^{2}\cos^{2}\frac{\varphi}{2};\]
\[AB = \sqrt{d^{2}\cos^{2}\frac{\varphi}{2}} = d \cdot \cos\frac{\varphi}{2};\]
\[R = \frac{\text{AB}}{2\pi} = \frac{d \cdot \cos\frac{\varphi}{2}}{2\pi}.\]
\[S_{бок} = 2\pi \cdot \frac{d \cdot \cos\frac{\varphi}{2}}{2\pi} \cdot d \cdot \sin\frac{\varphi}{2} =\]
\[= d^{2}\sin\frac{\varphi}{2}\cos\frac{\varphi}{2} =\]
\[= \frac{1}{2}d^{2} \cdot 2\sin\frac{\varphi}{2}\cos\frac{\varphi}{2} =\]
\[= \frac{1}{2}d^{2}\sin\varphi.\]
\[S_{осн} = \pi R^{2} = \frac{\pi d^{2}\text{co}s^{2}\frac{\varphi}{2}}{4\pi^{2}} =\]
\[= \frac{d^{2}}{4\pi} \cdot cos^{2}\frac{\varphi}{2};\]
\[S_{полн} = S_{бок} + 2S_{осн} =\]
\[= \frac{1}{2}d^{2}\sin\varphi + 2 \cdot \frac{d^{2}}{4\pi} \cdot cos^{2}\frac{\varphi}{2} =\]
\[= \frac{d^{2}}{2}\left( \sin\varphi + \frac{1}{\pi}\text{co}s^{2}\frac{\varphi}{2} \right).\]
\[Если\ AA_{1} - основание;\]
\[AB - высота,\ то\ S_{бок}\ не\ \]
\[изменится.\]
\[S_{осн} = \pi R^{2} = \frac{d^{2}\text{si}n^{2}\frac{\varphi}{2}}{4\pi};\]
\[S_{полн} =\]
\[= \frac{1}{2}d^{2}\sin\varphi + 2 \cdot \frac{d^{2}\text{si}n^{2}\frac{\varphi}{2}}{4\pi} =\]
\[= \frac{1}{2}d^{2}\sin\varphi + \frac{d^{2}}{2\pi} \cdot sin^{2}\frac{\varphi}{2}.\]
